 Samengestelde interest of rente op rente: een onderwerp, dat regelmatig weer vragen oproept. Zijn daar in Excel nu wel of niet functies voor?
Samengestelde interest of rente op rente: een onderwerp, dat regelmatig weer vragen oproept. Zijn daar in Excel nu wel of niet functies voor?
De aanleiding om hier over te schrijven was de volgende vraag:
“Volgens Microsoft-informatie bestaat er geen functie voor samengestelde interest in Excel.
Vroeger, al weer 50 jaar geleden, heb ik op de middelbare school nog financiële rekenkunde gekregen.
Daarbij gebruikte je de diverse rentetabellen met de diverse percentages om een bepaald bedrag uit te kunnen rekenen. Dat waren de kleine en grote A- en S-tabellen, als ik het mij nog goed herinner.”
In dit artikel zal ik laten zien, dat Microsoft zichzelf iets tekort doet. Het hangt van de situatie af. Maar zo gauw het wat ingewikkelder wordt, zul je toch zelf een systeem in Excel moeten bouwen, een soort (complexe) rentetabellen.
Rente op rente, variant 1a
Voor samengestelde interest zijn allerlei varianten denkbaar.
De meest eenvoudige is de situatie, dat u een bedrag op een spaarrekening zet waar jaarlijks een rente wordt bijgeschreven (ja, dat bestaat nog!). U laat na het eerste jaar alles op de rekening staan en krijgt in het tweede jaar dus ook rente vergoed over de rente van het eerste jaar (vandaar de naam Rente op rente).
 Nou dit is zo simpel, dat we daar ook eigenlijk geen functie voor nodig hebben.
Nou dit is zo simpel, dat we daar ook eigenlijk geen functie voor nodig hebben.
Op het einde van het eerste jaar wordt er rente bijgeschreven; uw tegoed is dan Bedrag * (1 + Rente%).
Op het einde van het tweede jaar wordt dit resultaat weer vermenigvuldigd met (1 + Rente%). Het mag duidelijk zijn, dat op het einde van de looptijd de Toekomstige Waarde gelijk is aan het gestorte Bedrag maal (1 + Rente%) tot de macht Looptijd.
 In het Voorbeeldbestand in het tabblad TW1 staat deze berekening van de Toekomstige Waarde in cel C8:
In het Voorbeeldbestand in het tabblad TW1 staat deze berekening van de Toekomstige Waarde in cel C8:
=Bedrag*(1+Rente)^Looptijd
In de formule staan geen celverwijzingen; de betreffende cellen C4 t/m C6 hebben een naam gekregen waardoor formules die daar naar verwijzen veel beter leesbaar zijn.
NB1 de eenvoudigste manier om een cel een naam te geven is door deze cel te selecteren en dan in het naamvak linksboven de gewenste naam in te tikken.
NB2 cellen met een groene achtergrond zijn invoer-cellen.
NB3 de vraag bovenaan het tabblad is dynamisch; in cel B1 staat de formule
=”Wat is “&Bedrag&” euro over “&Looptijd&” jaar waard bij “&TEKST(Rente;”0,0%”)&” rente?”
M.b.v. het &-teken worden teksten tussen aanhalingstekens samengevoegd met namen van cellen. Om te zorgen dat Rente een mooie opmaak krijgt is gebruik gemaakt van de functie TEKST.
NB4 misschien wat verwarrend: in dit geval wordt het woord Rente gebruikt waar een rentepercentage wordt bedoeld.
Rente op rente, variant 1b
Maar de berekening kan ook met de standaard Excel-functie TW uitgevoerd worden. De benodigde formule staat in cel C9 van het tabblad TW1 van het Voorbeeldbestand:
=TW(Rente;Looptijd;0;-Bedrag)
Zoals u ziet kent deze functie 4 parameters; de betekenis van de eerste 2 moge duidelijk zijn. Met de derde parameter kunt u aangeven of er nog vaste periodieke betalingen plaats vinden (in dit voorbeeld niet; hier komen we later nog op terug). De vierde parameter geeft aan wat de Huidige Waarde is; in dit voorbeeld ‘geven’ we dit bedrag aan de bank, vandaar het minteken.
LET OP1 als het minteken wordt weggelaten wordt het resultaat van de formule negatief.
LET OP2 als na het invoeren van de TW-functie op Enter wordt gedrukt, zal Excel het resultaat van de formule weergeven. Maar dat niet alleen: ook wordt de opmaak van de cel gewijzigd in Valuta.
Rente op rente, variant 1c
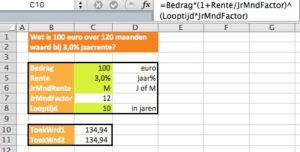 In de vorige voorbeelden is gewerkt met een jaarlijkse bijschrijving van de rente. In het tabblad TW2 van het Voorbeeldbestand kunt u zien wat het effect is van de verrekening van een maandrente (jaarrente gedeeld door 12). Afhankelijk van de keuze in cel C6 (J of M is mogelijk) wordt de JrMndFactor in cel C7 gelijk aan 1 of 12.
In de vorige voorbeelden is gewerkt met een jaarlijkse bijschrijving van de rente. In het tabblad TW2 van het Voorbeeldbestand kunt u zien wat het effect is van de verrekening van een maandrente (jaarrente gedeeld door 12). Afhankelijk van de keuze in cel C6 (J of M is mogelijk) wordt de JrMndFactor in cel C7 gelijk aan 1 of 12.
NB als er met maandrente wordt gerekend moet de looptijd niet in jaren maar in maanden worden uitgedrukt.
Rente op rente, variant 2
 Maar wat als er niet één storting plaats vindt, maar ieder jaar (aan het begin) een overboeking plaats vindt?
Maar wat als er niet één storting plaats vindt, maar ieder jaar (aan het begin) een overboeking plaats vindt?
Over het eerste bedrag wordt het aantal keren, dat de Looptijd is, rente uitgekeerd; over de tweede storting 1 keer minder etc. Met behulp van een wiskundige afleiding kan ook hier de TW uitgedrukt worden in een formule.
NB voor de liefhebbers: TW = Bedrag*(1+r)^n + Bedrag*(1+r)^n-1 + .. + Bedrag*(1+r).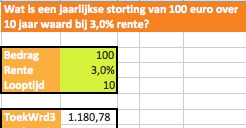 Vermenigvuldig deze vergelijking met (1+r) en trek ze van elkaar af. Allerlei termen vallen dan tegen elkaar weg. Nog wat reshuffelen en klaar is Kees.
Vermenigvuldig deze vergelijking met (1+r) en trek ze van elkaar af. Allerlei termen vallen dan tegen elkaar weg. Nog wat reshuffelen en klaar is Kees.
In het Voorbeeldbestand is deze formule in cel C8 van het tabblad TW3 opgenomen.
Maar ook hier kunnen we de standaard Excel-functie TW gebruiken; zie cel C9 in het tabblad TW3:
=TW(Rente;Looptijd;-Bedrag;0;1)
Omdat het hier periodieke betalingen/stortingen betreft, wordt het bedrag in de derde parameter geplaatst (met een min-teken). De vierde parameter (de huidige of startwaarde) is in dit geval 0.
NB de functie TW kent een optionele vijfde parameter (Type). Als deze 1 is dan betreft het een storting aan het begin van iedere periode (prenumerando); wordt hier 0 ingevuld of wordt deze weggelaten dan stelt het een storting op het einde van de periodes weer (postnumerando).
 Bij alle bovenstaande methodes is het nadeel, dat er telkens slechts het resultaat na één looptijd zichtbaar is.
Bij alle bovenstaande methodes is het nadeel, dat er telkens slechts het resultaat na één looptijd zichtbaar is.
In dit soort situaties is het vaak veel prettiger om een overzicht/systeem op te zetten, waar het verloop in de tijd zichtbaar is.
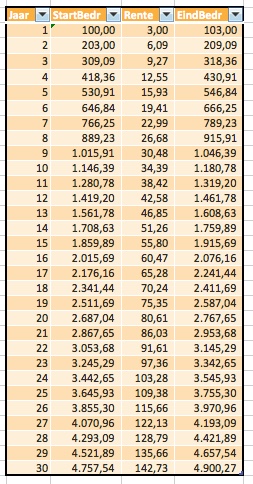
Op het tabblad TW3 in het Voorbeeldbestand staat zo’n systeem:
- het startbedrag van het eerste jaar is het stortingsbedrag uit cel C4: =Bedrag
- in de kolom daarnaast wordt de rente over jaar 1 berekend: =[@StartBedr]*Rente
dus het startbedrag uit dezelfde regel (vandaar de @) maal de rente uit cel C5 - in de volgende kolom staat het resultaat op het einde van het jaar: =[@StartBedr]+[@Rente]
- het startbedrag voor jaar 2 wordt dan het eindresultaat van jaar 1 plus de nieuwe storting: =H5+Bedrag
- aangezien we alles in de vorm van een Excel-tabel hebben gezet, worden de formules in de rente- en eind-kolom automatisch ingevuld
- de formule uit punt 4 kan naar beneden gekopieerd worden
Bij wijziging van het stortingsbedrag en/of rente-percentage zien we nu in één oogopslag wat de consequentie daarvan is in de loop van de tijd.
Rente op rente, variant 3a
 Maar wat als de stortingen en/of het rentepercentage nu niet meer constant zijn in de loop van de tijd?
Maar wat als de stortingen en/of het rentepercentage nu niet meer constant zijn in de loop van de tijd?
In het tabblad TW4 van het Voorbeeldbestand is het systeem uit het tabblad TW3 iets aangepast: er zijn kolommen voor het stortingsbedrag en het rentepercentage bij gekomen.
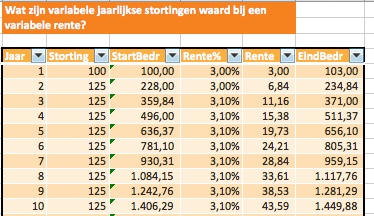 NB in deze 2 nieuwe kolommen staan alleen in de eerste rij ‘harde’ waarden (namelijk 100, respectievelijk 3%); daaronder staan altijd verwijzingen naar de regel daarboven. Een wijziging in één van de jaren wordt dan automatisch naar de toekomst doorgevoerd.
NB in deze 2 nieuwe kolommen staan alleen in de eerste rij ‘harde’ waarden (namelijk 100, respectievelijk 3%); daaronder staan altijd verwijzingen naar de regel daarboven. Een wijziging in één van de jaren wordt dan automatisch naar de toekomst doorgevoerd.
Rente op rente, variant 3b
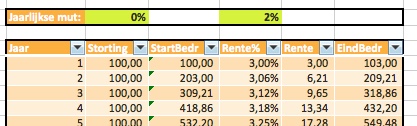 Op het tabblad TW4 staat nog een tweede systeem.
Op het tabblad TW4 staat nog een tweede systeem.
We weten natuurlijk niet exact welk bedrag we in de toekomst kunnen sparen en wat de rente zal zijn. Maar we kunnen wel schattingen maken: ieder jaar denken we 10% meer te kunnen sparen (in het voorbeeld staat deze schatting nog op 0%) en we verwachten (hopen?), dat de rente ieder jaar 2% zal stijgen (relatief dus, geen harde 2%. In dat geval hadden we gezegd, dat het percentage met 2 procent-punt zou stijgen).
Welke van bovenstaande varianten de voorkeur heeft, is natuurlijk afhankelijk van uw eigen wensen. Betreft het slechts een eenmalige berekening of is er veel flexibiliteit en inzicht gewenst etcetera.

