Voorspellen. Wat zou het mooi zijn als we dat zouden kunnen! Tenminste, als die voorspellingen ook nog eens betrouwbaar zouden zijn.
In het dagelijks leven vliegen ons de voorspellingen om de oren: of het nu gaat over het weer, de voetbaluitslagen, de ontwikkelingen rond Corona.
Ook na het analyseren van cijfers komen er vaak vervolgvragen: hoe zullen de verkoopcijfers er op het einde van het jaar uitzien, hoe ziet de gemiddelde temperatuur er over 10 jaar uit etcetera.
We hebben al eerder laten zien dat je in Excel snel en eenvoudig trend-analyses kunt maken: Trend-analyse en Klimaat-streepjescode. Maar daarbij ging het altijd om lineaire trends.
In dit artikel zullen we laten zien, dat je met Excel ook niet-lineaire trends kunt bepalen.
Lineaire trend
Voordat we niet-lineaire trends gaan bekijken toch nog even naar de simpele voorspelling (lineair).
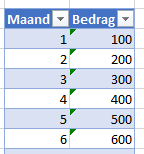
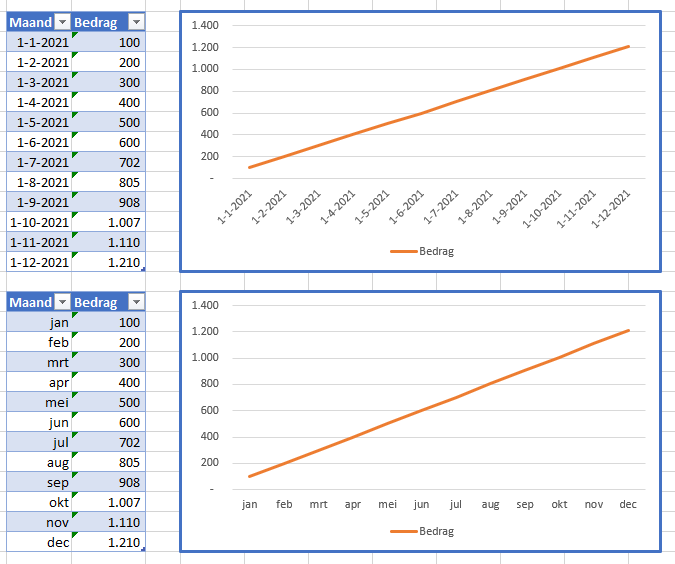
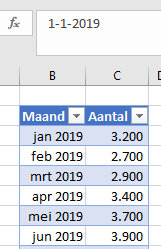
We beginnen met een simpel voorbeeld: we hebben een overzicht van de eerste 6 maanden van het jaar met de bijbehorende bedragen (zie het tabblad Lin van het Voorbeeldbestand).
Als we zouden moeten ‘gokken’ hoe de ontwikkeling de maanden daarna zal zijn, komen we daar wel uit: iedere maand komt er 100 bij.
LET OP uiteraard alleen onder de aanname dat de ontwikkeling in het verleden zich voortzet in de toekomst!
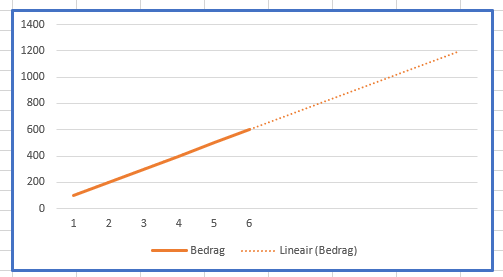
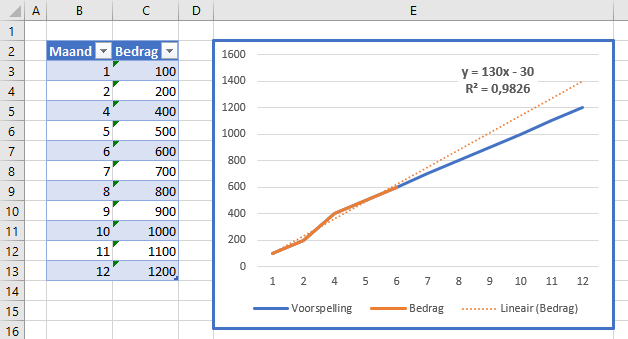
In de grafiek van deze gegevens hebben we Excel ook een trendlijn laten tekenen, die we laten doorlopen tot het eind van het jaar (zie voor de werkwijze het artikel Trend-analyse).
Ook Excel komt tot de conclusie dat in maand 12 het bedrag waarschijnlijk gelijk is aan 1200.
LET OP2 we hebben hier (uiteraard) een lineaire trendlijn gekozen.
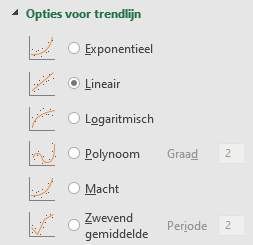
Dit kun je wijzigen in het scherm Opties voor trendlijn (klik rechts op een trendlijn en kies de optie Trendlijn opmaken).
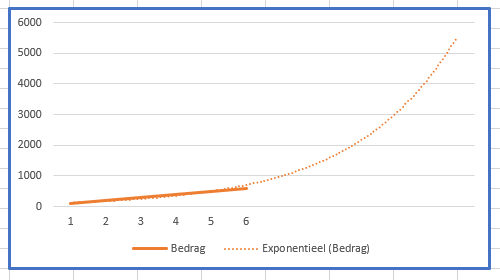
Kies je in dit geval bijvoorbeeld de optie Exponentieel dan zal de verwachting voor de rest van het jaar er heel anders uitzien!
Het is dus altijd zaak om bij voorspellingen aan te geven welke methode is gebruikt.
Maar we hoeven niet per se een trendlijn te laten tekenen; we kunnen de ‘voorspelling’ van de toekomst ook met behulp van Excel-formules bepalen.
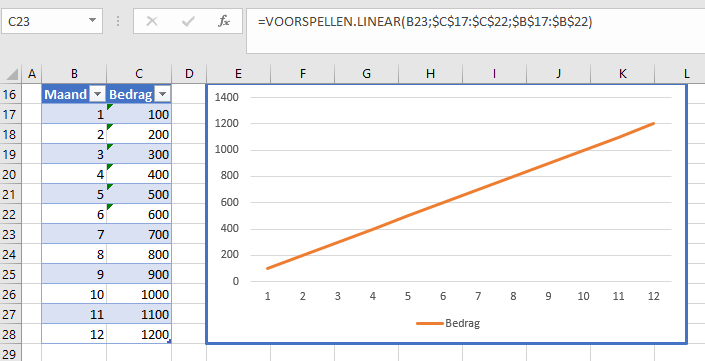
In cel C23 van het tabblad Lin in het Voorbeeldbestand staat de formule:
=VOORSPELLEN.LINEAR(B23;$C$17:$C$22;$B$17:$B$22)
Ofwel: voorspel, op basis van een lineaire trend, vanuit de waarden in de cellen C17:C22, die horen bij de maanden in de cellen B17:B22, wat het bedrag zal zijn in de maand in cel B23.
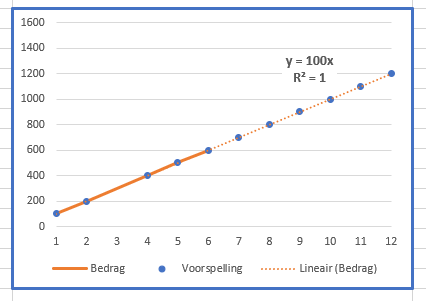
Wanneer we deze formule naar beneden kopiëren, ontstaat een grafiek vergelijkbaar met het vorige voorbeeld, inclusief trendlijn.
NB bij het vertalen vanuit de Engelstalige versie heeft Microsoft in de functienaam een i over het hoofd gezien!
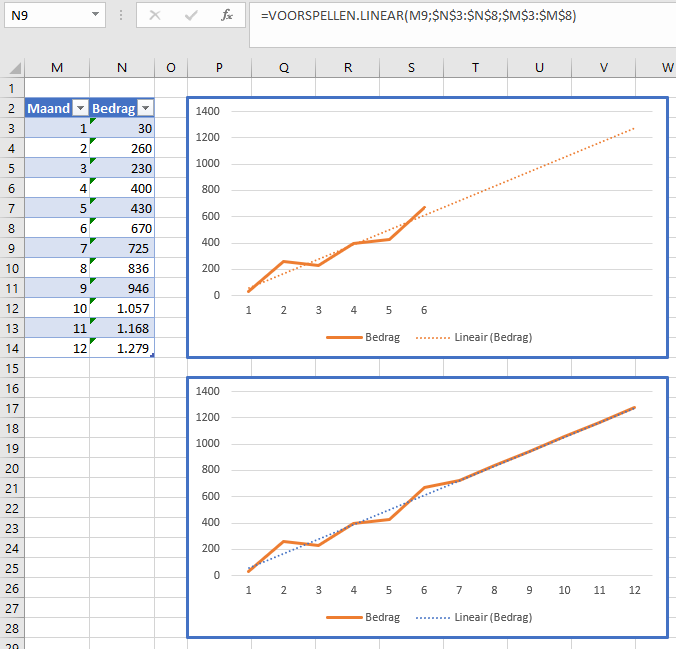
Als we op dezelfde manier als hiervoor grafieken maken op basis van minder ‘gladde’ gegevens, dan wordt duidelijk dat de methodieken van een lineaire trendlijn en de functie Voorspellen.Linear gelijk zijn (zie het tabblad Lin van het Voorbeeld-bestand).
Functie Voorspellen
Voordat we dieper ingaan op het gebruik van de Voorspellen-functies, moeten we eerst wat haken en ogen bespreken.
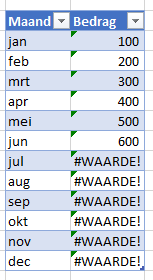
In de vorige voorbeelden werden de maanden met getallen aangegeven. Wanneer we de (duidelijkere) notatie met afkortingen gebruiken, werkt de Voorspellen-functie niet meer!
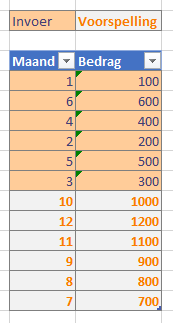
Zie het tabblad Voorspelling van het Voorbeeldbestand.
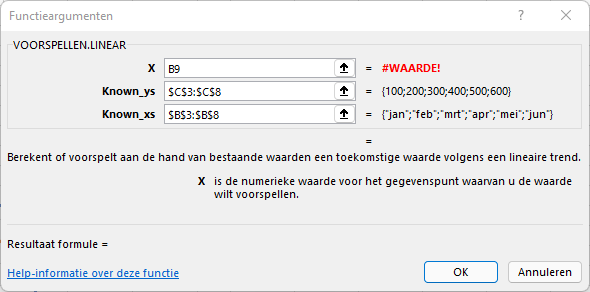
Zoals uit het scherm Functieargumenten blijkt (gebruik de ![]() naast de formulebalk) verwacht Excel numerieke waarden (getallen dus) voor de onafhankelijke x-waarden; ook voor de daarvan afhankelijke y-waarden trouwens.
naast de formulebalk) verwacht Excel numerieke waarden (getallen dus) voor de onafhankelijke x-waarden; ook voor de daarvan afhankelijke y-waarden trouwens.
NB ook hier zien we dat de vertalers wat steken hebben laten vallen; tenminste in mijn Excel-versie (2019).
Gelukkig kunnen we aan het #WAARDE!-probleem wel wat doen (zie het tabblad Voorspelling van het Voorbeeldbestand):
Aangezien een datum voor Excel ‘gewoon’ een getal is, is dit probleem te tackelen door in plaats van een maandaanduiding de eerste dag van de maand in te voeren. In het tweede blok hebben we de cellen van de Maand-kolom een zodanige notatie gegeven, dat alleen de maandaanduiding overblijft (gebruik daarvoor de Cel-eigenschappen, Ctrl-1).
NB1 je zou in de maandaanduiding overal ook bijvoorbeeld de 2e dag van de maand kunnen nemen.
NB2 Wat opvalt aan de nieuwe cijfers is dat de functie Voorspellen wat meer ‘intelligentie’ heeft meegekregen. Doordat tussen de diverse begindatums van de maanden niet iedere keer even veel dagen zitten, is de maandelijkse toename in de voorspelling niet precies 100.
Wat kun je als waarden voor de onafhankelijke reeks (de x-waarden) gebruiken?
- Zoals we hebben gezien kan de reeks uit aansluitende getallen bestaan (1 ,2 ,3 … of 26, 27, 28 …. etc).
Ook opeenvolgende datums zijn intern voor Excel opeenvolgende getallen.
Maar ook 10, 20, 30 … werkt; als er maar een gelijke stap tussen de getallen zit; dus ook 4-1-2021, 11-1-2021, 18-1-2021 … (een serie maandagen op een rij). - Ook hebben we gezien dat Excel het snapt als de reeks bestaat uit de eerste dag van opvolgende maanden (mag ook de 2e of 3e zijn etc.). Het moeten dus logische intervallen zijn.
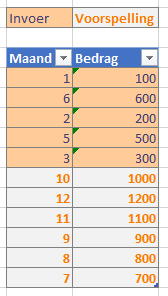
NB3 de functie Voorspellen werkt ook als de brongegevens niet in de juiste volgorde staan (zie het tabblad Voorspelling). Maar waarom je dat zou doen?
NB4 ook als er één of meerdere waarden ontbreken dan levert de functie nog steeds (de juiste) resultaten.
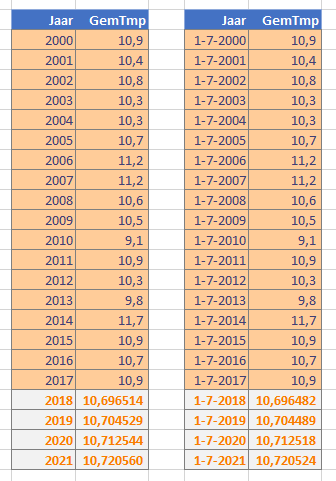
LET OP heb je jaarcijfers (zoals hiernaast de gemiddelde jaartemperaturen in De Bilt) dan maakt het voor de voorspelling wel uit of je in de onafhankelijke kolom een jaaraanduiding gebruikt of een consistente datum in het betreffende jaar.
In dit geval zijn de verschillen minimaal; pas significant in de 5e decimaal.
Ontbrekende gegevens
Zoals we hiervoor hebben gezien werken de Voorspellen-functies ook als er ‘gaten’ zitten in de tijdlijn.
Laten we nog eens een voorbeeld nemen (zie het tabblad Ontbrekend in het Voorbeeldbestand). De gegevens van maand 3 ontbreken, maar de Voorspellen.Linear-functie (vanaf maand 7) herkent toch het juiste lineaire verloop. Dit in tegenstelling tot de trendlijn in de grafiek; die loopt te steil!
Dit probleem wordt veroorzaakt omdat de x-as in bovenstaande grafiek niet juist het tijdsverloop weergeeft.
Kiezen we als grafiektype het Spreidingsdiagram (soms x-y-grafiek genoemd), dan zien we dat ook de trendlijn het verwachte verloop vertoont.
Ook op een andere manier kunnen we zien dat Excel rekening houdt met ‘gaten’ in de gegevens:
- we starten met de basis-gegevens in het tabblad Ontbrekend van het Voorbeeldbestand.
- dus selecteer de cellen B2:C7
- kies in de menutab Gegevens in het blok Voorspelling de optie Voorspellingsblad
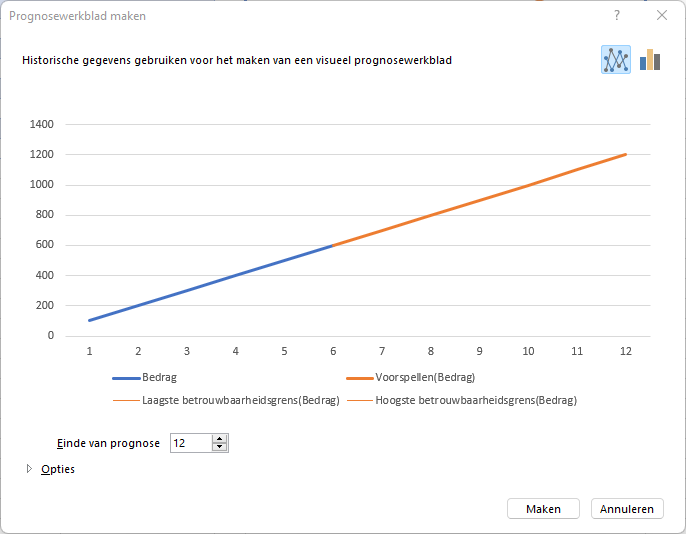
- we willen ook de voorspelling van maand 12 weten: maak Einde van prognose gelijk aan 12 en druk op de button Maken.
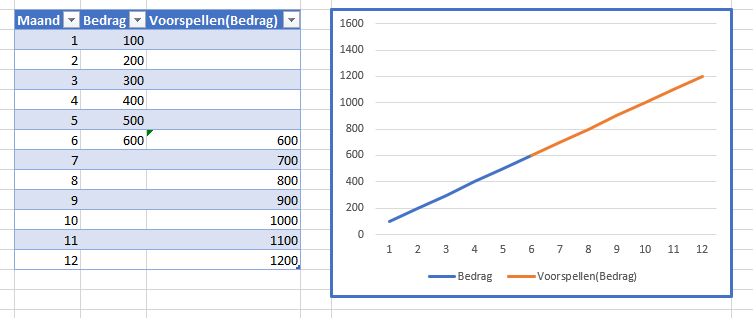
Excel maakt een nieuw tabblad aan met daarin een gegevens-tabel en een grafiek. In de gegevenstabel zien we dat ook maand 3 een bedrag heeft gekregen! En we hebben een aparte kolom voor de voorspellingen (om de 2 stukken in de grafiek netjes te laten aansluiten is de eerste ‘voorspelling’ gelijk aan het bedrag in die maand).
NB Excel gebruikt in dit geval voor de voorspelling niet Voorspellen.Linear maar een meer algemeen bruikbare methode: de AAA-versie van het algoritme ETS (Exponential Triple Smoothing). In cel I9 staat dan ook de formule =VOORSPELLEN.ETS(G9;$H$3:$H$8;$G$3:$G$8;1;1).
Verderop in dit artikel zoomen we verder in op deze functie.
ETS versus lineair
Om het verschil tussen deze 2 methodes (en het gevaar van de lineaire benadering) te beoordelen, staat in het tabblad Basis van het Voorbeeldbestand een maandoverzicht met daarbij behorende aantallen.
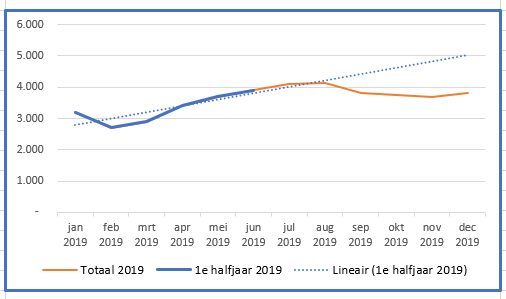
Maken we van de eerste 6 maanden een grafiek met daarin een lineaire trendlijn dan verwachten we op het einde van 2019 een aantal van ongeveer 5.000.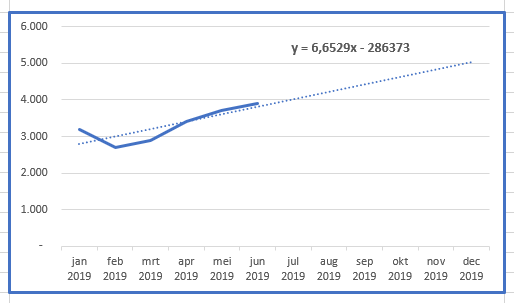
Maar uit het jaaroverzicht blijkt dat die voorspelling er behoorlijk naast zit.
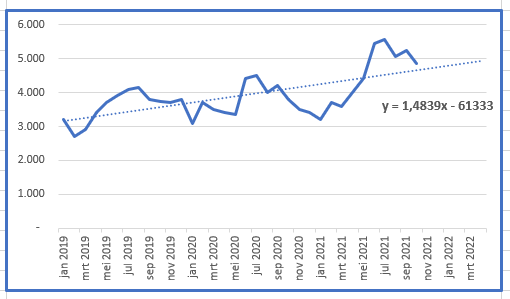
Wanneer we alle bekende gegevens meenemen (tot en met okt 2021) en we laten Excel een lineaire trendlijn bepalen dan halen we misschien in maart 2022 de 5.000.
Maar wat is van zo’n voorspelling nu de betrouwbaarheid? Daar kan ETS een uitkomst bieden:
- selecteer op het tabblad Basis de cellen B2:C8
- kies in de menutab Gegevens in het blok Voorspelling de optie Voorspellingsblad
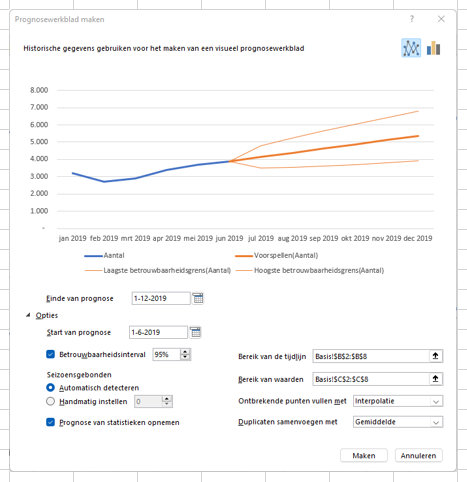
- open op het tussenscherm onderaan Opties
- pas het Einde van prognose aan
Op dit tussenscherm zie je al een grafische voorstelling van de voorspelling. Niet alleen het verwachte verdere verloop van de aantallen, maar ook een inschatting van de betrouwbaarheid van deze voorspelling.
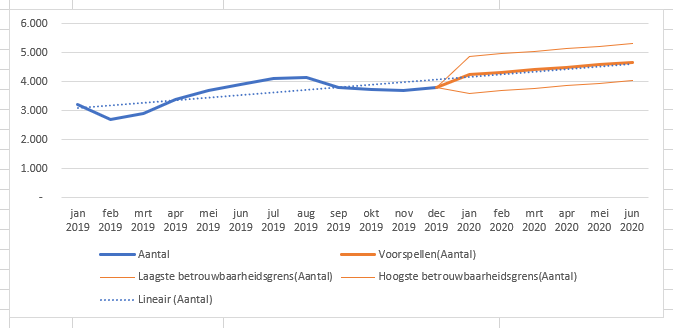
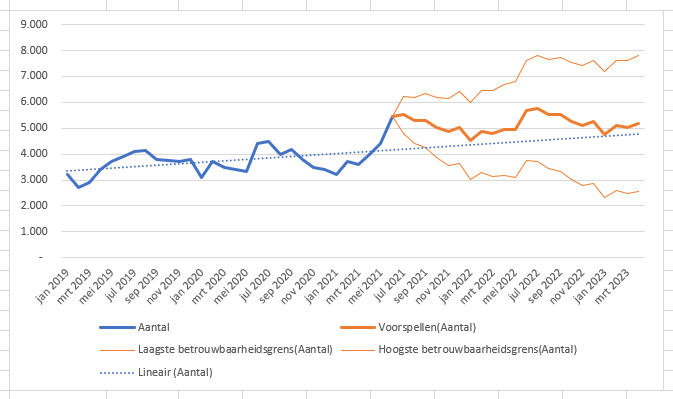
Op basis van de gegevens van de eerste 6 maanden van 2019 verwacht ETS dat 95% van de toekomstige aantallen binnen de 2 dunne oranje lijnen zullen liggen (zie het tabblad GegHalfJaar van het Voorbeeldbestand).
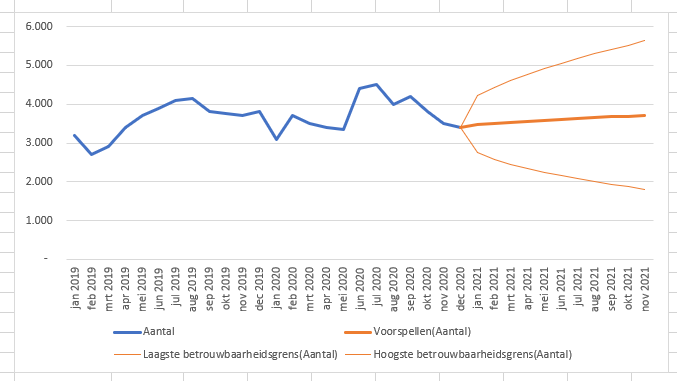
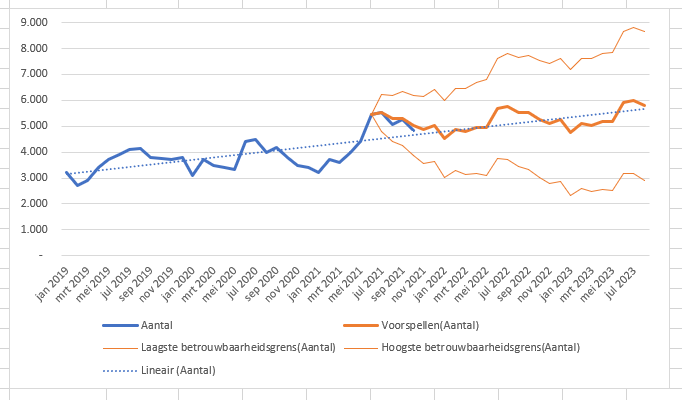
Doen we hetzelfde met de gegevens van heel 2019 dan krijgen we het volgende resultaat (zie het tabblad GegJaar van het Voorbeeldbestand):
De volgende opmerkingen horen bij deze twee voorbeelden:
- de betrouwbaarheid van de voorspelling zie je duidelijk beter worden: het verschil tussen de 2 dunne lijnen op het einde van de tweede grafiek is ongeveer 1270, terwijl dat in het voorbeeld hiervoor meer dan het dubbele is.
- in allebei de gevallen kiest de ETS-methode een lineaire benadering voor de voorspellingen
- bij de gegevens van een half jaar worden de voorspellingen in de loop van de tijd steeds ‘slechter’; de twee dunne lijnen lopen steeds verder uit elkaar.
De gegevens van een heel jaar zijn van dien aard dat de betrouwbaarheidsgrenzen in de maanden daarna overal ongeveer even ver van de voorspelling af blijven liggen.
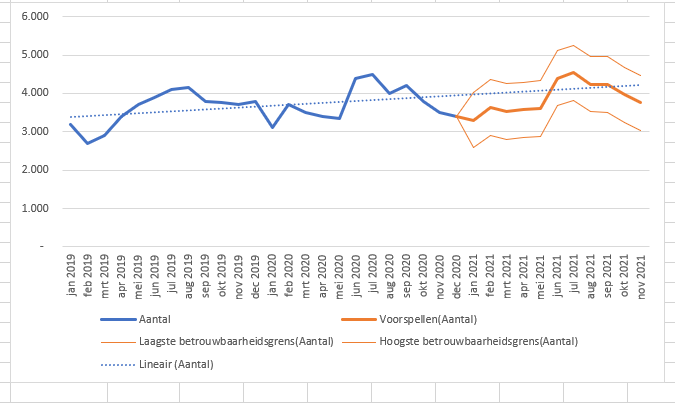
Wat als we de gegevens van 2 jaar gebruiken voor de voorspellingen?
Op het tabblad Geg2Jaar van het Voorbeeldbestand is te zien, dat de ETS-methode nog steeds uitgaat van een lineair verloop. De fluctuaties in de loop van de tijd zorgen er wel voor dat de betrouwbaarheidsgrenzen weer uit elkaar gaan lopen.
Maar zou er ook een seizoenspatroon in kunnen zitten? Een piek(je) in het midden van het jaar? Dat kunnen we gelukkig in Excel ook uitproberen: in de Opties zetten we het aantal bij Seizoensgebonden op 12 (zie het tabblad Geg2jaarb).
Het lineaire verloop in de voorspelling is daarmee (uiteraard) verdwenen en het betrouwbaarheidsinterval is beduidend smaller geworden! Een indicatie dat de kwaliteit van de voorspelling vooruit is gegaan.
NB meestal zal de ETS-methode pas na 2 seizoen-cycli niet meer de lineaire benadering toepassen op de voorspelling.
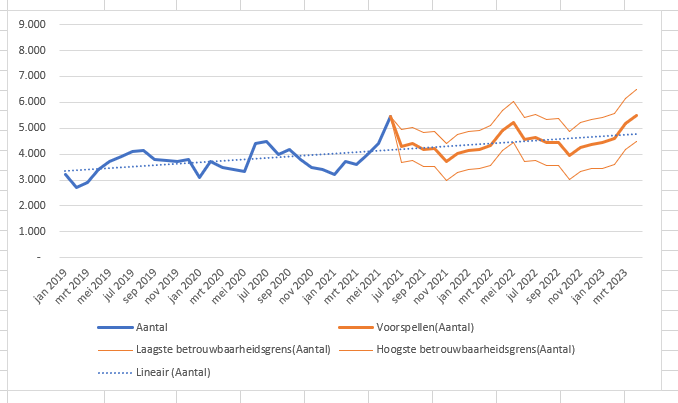
Bovenstaande grafieken zijn gemaakt op basis van gegevens van 2½ jaar. De linkse ontstaat wanneer Excel automatisch de berekeningen uitvoert (zie het tabblad Geg2,5Jaar van het Voorbeeldbestand). Blijkbaar ontstaat de beste fit wanneer een seizoenspatroon van 11 maanden wordt gekozen.
De rechtse grafiek ontstaat wanneer we uitgaan van een seizoenspatroon van 1 jaar (zie tabblad Geg2,5Jaarb). Dat lijkt in ieder geval reëler, maar duidelijk is te zien dat de betrouwbaarheid van de voorspellingen dan verslechteren.
Op het laatste tabblad (Geg2,5Jaarc) zien we de voorspellingen, op basis van gegevens van 2½ jaar, aangevuld met de resultaten van de meest recente maanden.
Het lijkt er op, dat de voorspelling op basis van een 12-maanden seizoen zo gek nog niet is.
LET OP door bovenstaande voorbeelden mag het duidelijk zijn dat het ‘gevaarlijk’ is om te vertrouwen op één manier van voorspellen. En logisch: hoe meer historische gegevens hoe beter de voorspelling zal zijn. Tenminste als de gegevens in een stabiele omgeving zijn verzameld (we zullen deze voorspellingsmethode dus maar niet loslaten op de Corona-cijfers).
NB1 Op het Opties-blad kun je ook aangeven hoe groot het betrouwbaarheidsinterval moet zijn: ![]()
NB2 de ETS-methode kent diverse betrouwbaarheidsstatistieken: ![]()
Het resultaat daarvan zie je in de diverse tabbladen: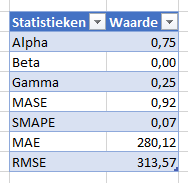
Kijk voor de betekenis van deze parameters bijvoorbeeld op
exceljet.net/excel-functions/excel-forecast.ets.stat-function of
www.brightworkresearch.com/alpha-beta-and-gamma-in-forecasting/.