Soms overkomt het je: krijg je een Excel-vraag en er gaat een heel nieuwe wereld voor je open.
Een paar weken geleden kreeg ik de vraag hoe je er voor zorgt dat, bij het uitzetten van een te vliegen traject, bij het berekenen van een gecorrigeerde koers er geen negatieve waarden of waarden groter dan 360o ontstaan.
Redelijk eenvoudig, maar toen kwam de volgende vraag: kun je gecorrigeerde koersen ook in Excel berekenen?
Na wat over en weer mailen werd het me duidelijk dat het een amateur-vlieger (zeg je dat zo?) heel wat tijd kost voordat hij kan gaan vliegen: routes, koersen moeten van te voren worden uitgestippeld, een zogenaamde vluchtlog moet worden opgesteld etcetera.
Maar zo’n nieuwe wereld is dan weer mooi een aanleiding om een Excel-artikel te schrijven.
Opmaak koersen
Bij het invullen van een vluchtlog moet niet alleen de koers worden uitgestippeld, ook moet deze theoretische koers nog gecorrigeerd worden voor wat betreft het effect van wind. Voor ons buitenstaanders: als de wind van rechts komt, dan zullen we ook iets meer naar rechts moeten ‘sturen’ dan de theoretische koers aangeeft.
Bij zo’n correctie kan het natuurlijk voorkomen dat we een koers kleiner dan 0 of groter dan 360 krijgen; dat moet dan nog aangepast worden.
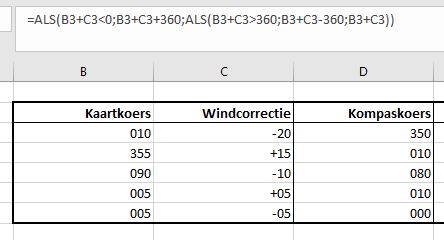
In het Voorbeeldbestand op het tabblad KK staat een recht toe recht aan berekening. In kolom B staat de kaartkoers (theoretische koers), in kolom C is de correctie vanwege de wind opgenomen. In kolom D tellen we die 2 waardes op. Maar als die optelling negatief is, dan tellen we er nog eens 360 bij op. Wordt de som groter dan 360 dan trekken we er 360 vanaf.
Dit was eigenlijk de oorspronkelijke vraag, die ik kreeg. Maar uit onze correspondentie bleek, dat vliegeniers gewend zijn om koersen altijd met 3 getallen weer te geven en de correctie krijgt altijd een + of – teken.
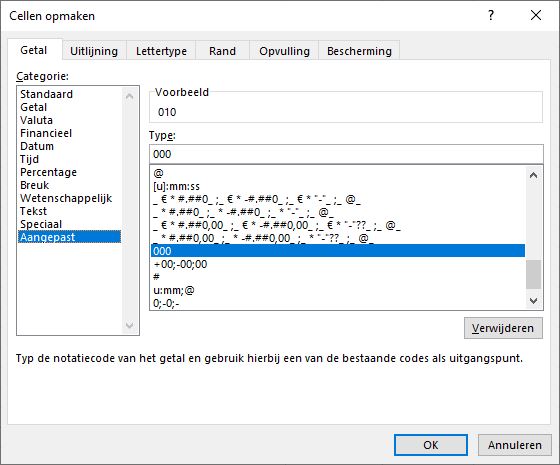
Het eerste is in Excel snel opgelost. De cellen met koersen krijgen allemaal de opmaak zoals hiernaast weergegeven:
- selecteer de cellen die dezelfde opmaak moeten krijgen (eventueel Ctrl ingedrukt houden als de cellen niet aaneengesloten zijn)
- klik rechts en kies Celeigenschappen (of druk op Ctrl-1)
- kies de categorie Aangepast
- en het veld onder Type krijgt de waarde 000 (dus altijd 3 cijfers weergeven)
Om het tweede ‘probleem’ op te lossen krijgen de cellen in kolom C een andere opmaak: ![]()
Met het gedeelte voor de eerste punt-komma geven we aan dat positieve getallen altijd 2 cijfers bevatten en van een plus-teken moeten worden voorzien; via het tweede blokje bepalen we hoe negatieve getallen er uit moeten zien en als laatste dat een nul-waarde door 2 nullen wordt weergegeven.
NB de inhoud van de cellen verandert hierdoor niet, we hebben alleen de opmaak aangepast.
Bij de berekening van de Kompaskoers (kolom D) hebben we een geneste Als-functie gebruikt. Zoals zo vaak: in Excel kunnen we dat ook op een kortere manier oplossen.
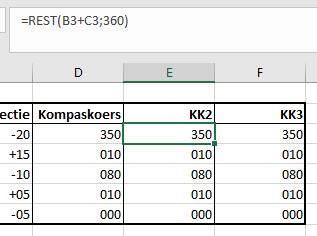
Met behulp van de functie Rest bepalen we wat er overblijft wanneer we delen door 360 en en het gehele deel ‘weggooien’. Bij getallen tussen 0 en 360 is de rest na deling het getal zelf, bij getallen groter dan 360 wordt er 360 vanaf getrokken.
Maar de formule werkt ook als de optelling een negatief getal oplevert!
Dat blijkt ook uit kolom F, waar we de werking van de Rest-functie hebben nagebootst:
=D3-360*GEHEEL(D3/360)
Windcorrectie
Na het beantwoorden van de eerste vraag, kreeg ik een mail terug met een dankwoord en de opmerking: “Maar de windcorrectie berekenen in Excel is zeker te ingewikkeld?“
Wat bleek: als de windsnelheid en -richting bekend zijn moeten er allerlei handmatige acties op aparte apparaten uitgevoerd worden om de windcorrectie te bepalen.
Eerste reactie mijnerzijds was: dat kan niet zo moeilijk zijn, een beetje rekenen met vectoren, daar hebben ze goniometrie voor uitgevonden! Maar dat viel toch wel tegen. Dus ik moet bekennen dat ik toen toch maar even Google heb gebruikt.
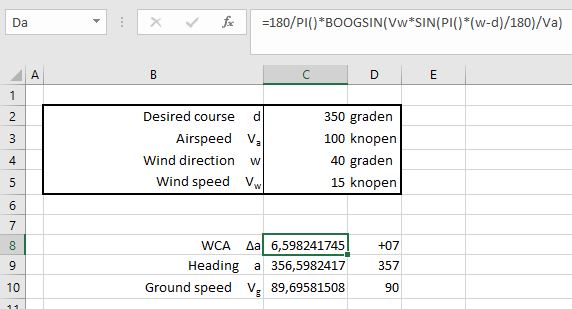
Op de site en.wikipedia.org/wiki/E6B vond ik het volgende (zie ook het tabblad Heading in het Voorbeeldbestand):

Op het tabblad Heading staat een voorbeeld van deze berekeningen.
NB zorg wel dat de snelheden in dezelfde eenheden zijn uitgedrukt!
Aangezien Excel binnen de goniometrische functies met radialen werkt is de 2e set formules gebruikt. De cellen in kolom C hebben een toepasselijke naam gekregen, zodat de formules beter leesbaar en dus beter controleerbaar zijn.
NB De Excel-vertaling van sin-1 is de functie Boogsin; de waarde voor π krijgen we door de functie Pi() te gebruiken.
In kolom D zorgen we voor een afronding naar gehele getallen: 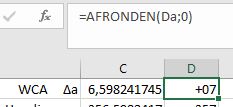
Uiteraard kunnen deze berekeningen ook in één keer (zie cel C15):
=AFRONDEN(180/PI()*BOOGSIN(Vw*SIN(PI()*(w-d)/180)/Va);0)
Vluchtlog
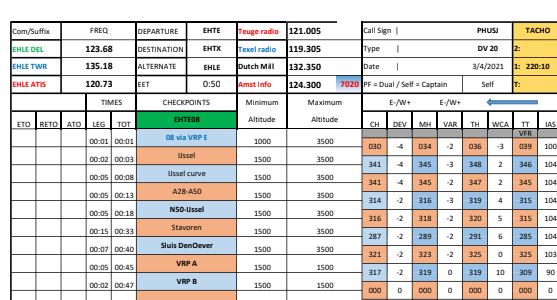
Als voorbeeld kreeg ik het voorbereidende materiaal voor een vlucht van Teuge naar Texel. Een uittreksel:
In het tabblad Route van het Voorbeeldbestand hebben we op basis van bovenstaande informatie de vluchtlog enigszins nagebouwd.
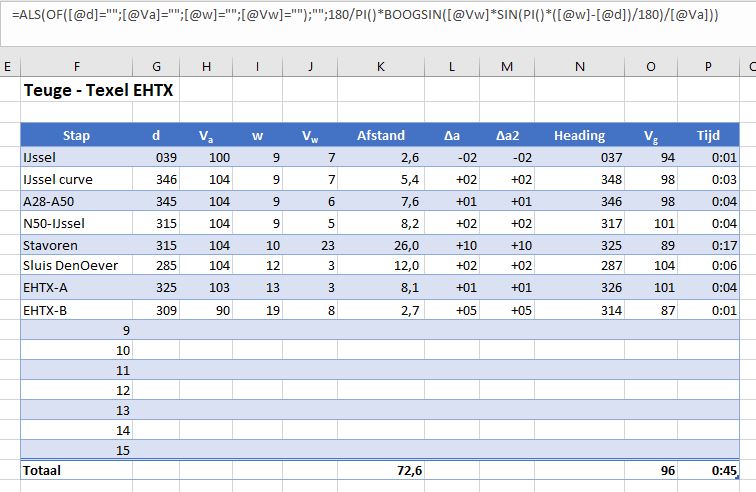
De vluchtlog is een Excel-tabel met de naam tblHeading. In de gebruikte formules wordt dan ook verwezen naar de kolom-koppen (een @ betekent: haal de waarde uit een kolom in dezelfde regel waar de formule staat). De formule in kolom L wordt alleen berekend als geen van de cellen in dezelfde regel in de kolommen G, H, I of J leeg is.
NB1 het rekenen met richtingen/graden gaat in de vliegerij iets anders dan in de wiskunde. Vliegen naar het noorden is richting 0o, naar het oosten 90o etc. Een windrichting betekent dat de wind vanuit die richting komt.
NB2 het omrekenen van graden naar radialen en vv kunnen we ook aan Excel overlaten (zie kolom M):
=ALS(OF([@d]=””;[@Va]=””;[@w]=””;[@Vw]=””);””;GRADEN(BOOGSIN([@Vw]*SIN(RADIALEN([@w]-[@d]))/[@Va])))
In kolom N wordt dan de te vliegen koers bepaald: =ALS([@∆a]=””;””;REST([@d]+[@∆a];360))
Uiteraard willen we ook weten hoelang we straks onder weg zullen zijn. In kolom O wordt de zogenaamde grondsnelheid bepaald, rekening houdend met wind mee of tegen:
=ALS([@Heading]=””;””;WORTEL([@Va]^2+[@Vw]^2-2[@Va][@Vw]COS(PI()([@d]-[@w]+[@∆a])/180)))
Dan kunnen we per stap (of in vliegtermen Leg) de benodigde tijd uitrekenen (kolom P):
=ALS([@Vg]=””;””;[@Afstand]/[@Vg]/24)
NB we delen ook nog eens door 24, omdat het resultaat van Afstand/snelheid het aantal uren is. Op deze manier komt in kolom P een waarde, die het dagdeel aangeeft. Door dan de cellen een opmaak van uren en minuten te geven is het resultaat voor ons makkelijk interpreteerbaar.
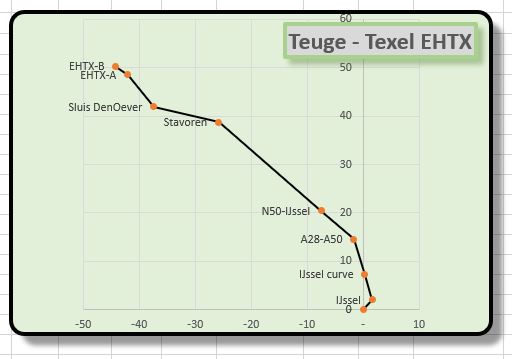
Route-grafiek
Nou we toch bezig zijn: we willen natuurlijk ook nog wel ‘zien’ hoe we gaan vliegen; een plaatje zou wel mooi zijn.
Alles kan! (?)
We moeten dan wel eerst de gewenste koers (dus NIET de te vliegen koers) vertalen naar wiskundige hoeken. Wat blijkt: dat is niet zo ingewikkeld, hoek = 90o – koers.
Aangezien de x-coördinaat van het eindpunt van een stap berekend kan worden via de cosinus van de hoek en de y-coördinaat met de sinus zijn we er al bijna.
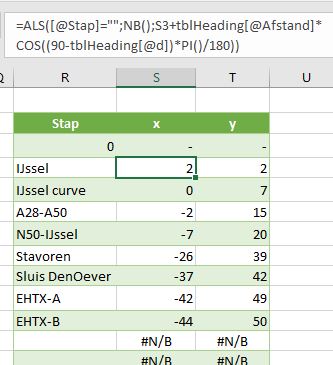
In kolom S op het tabblad Route van het Voorbeeldbestand worden de x-coördinaten van de stappen bepaald, in kolom T de y-coördinaten.
Door de vorige coördinaten daar telkens bij op te tellen krijgen we de vliegroute.
NB wanneer een stap niet gevuld is wordt met behulp van de functie NB() aangegeven dat die coördinaat niet bestaat. Bij het maken van een grafiek worden die punten niet meegenomen door Excel (zie Grafiek zonder nullen).
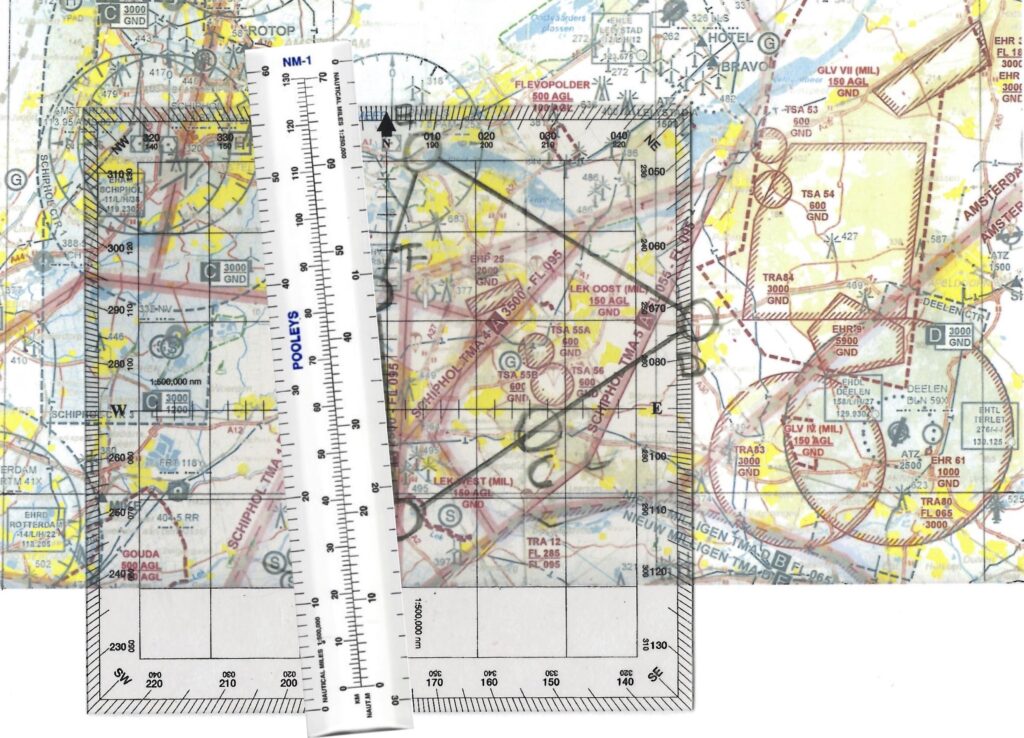
Op basis van deze tabel is bovenstaande grafiek gemaakt. Gebruik daarvoor een spreidingsdiagram.
NB1 het omrekenen van graden naar radialen gebeurt, ter illustratie, in de kolommen S en T op een verschillende manier.
NB2 door de grafiek te laten tekenen met vloeiende lijnen ontstaat een iets reëler beeld.
NB3 om een goede weergave van de vliegroute te krijgen moet je de hoogte en/of breedte van de grafiek zodanig aanpassen, dat de rasterlijnen vierkanten vormen.
NB4 disclaimer: ik ga er wel van uit dat piloten van bijvoorbeeld een 737 Max deze spreadsheet niet gaan gebruiken!
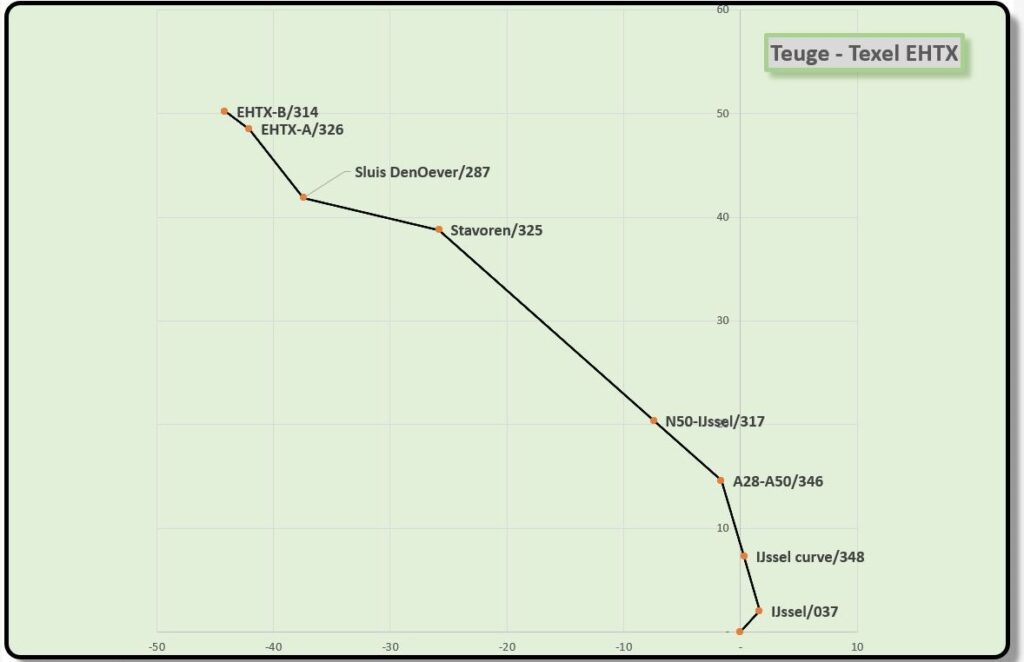
De labels van de grafiek kunnen bijvoorbeeld nog aangevuld worden met de te vliegen koers, zie het tabblad grafRoute van het Voorbeeldbestand.