Ik kreeg deze week van Hasan de volgende vraag in mijn mailbox:

Ik ben bezig met een lijngrafiek waarbij de waarde nul zichtbaar is in mijn grafiek. Dat wil ik niet. Hoe kan ik dat oplossen?

Meestal leiden er meerdere wegen naar Rome, maar hiervoor kan ik toch maar één oplossing bedenken. Kent iemand nog een alternatief?

Aan de hand van het (vereenvoudigde) voorbeeld van Hasan zal ik laten zien hoe de oplossing werkt.

Prognose versus realisatie

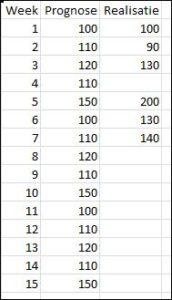Hasan heeft een overzicht per week (en maand en kwartaal) van budgetcijfers, prognoses en realisaties. Ik zal verder werken met alleen prognoses en realisaties (zie het tabblad Basis in het Voorbeeldbestand).

Zoals te zien is, kennen we de realisatie tot en met week 7; maar zit deze nou boven of onder de prognose?

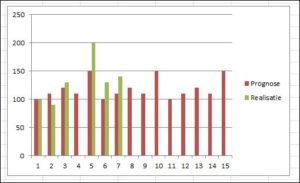
Misschien dat een grafische weergave meer inzicht geeft?

Tsja, dat helpt nog niet echt veel. Nee, we ontkomen er niet aan om naast bovenstaande cijfers ook met cumulatieven vanaf week 1 te gaan werken.

Prognose versus realisatie, incl. cumulatieven

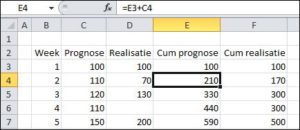Twee extra kolommen nemen de cumulatieve cijfers voor hun rekening (zie tabblad Cum1 in het Voorbeeldbestand):

1. in cel E3 komt dezelfde waarde als in C3
2. zoals te zien is, staat in E4 de formule
   =E3+C4
   ofwel: neem de vorige cumulatieve prognose (E3) en tel daar de prognose van de betreffende week bij op (C4)
3. deze formule wordt naar beneden gekopieerd
4. hetzelfde gebeurt in kolom F voor de realisatie

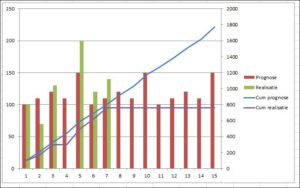Deze 2 kolommen aan de grafiek toevoegen; duidelijk (?) is te zien dat de totale realisatie (de paarse lijn) achter blijft bij de cumulatieve prognose (blauwe lijn).

Maar we kennen de realisatie t/m week 7 al; waarom dan nog met de prognose van die eerste weken rekenen om tot een cumulatieve prognose te komen? Zo is ook de cumulatieve realisatie na week 7 niet interessant.

Prognose versus realisatie, incl. cumulatieven (deel 2)

Daarom een nieuwe opzet gemaakt voor de cumulatieve kolommen (zie tabblad Cum2 in het Voorbeeldbestand):

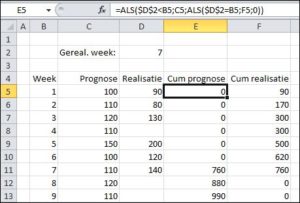
1. allereerst maken we het ons gemakkelijk en plaatsen we in cel D2 het laatste weeknummer waarvan we de realisatie kennen
2. in cel E5 komt de eerste ‘cumulatieve’ prognose; deze is  afhankelijk van D2. Als er nog geen realisatie is  (D2<B5) dan is de cumulatieve prognose gelijk aan de prognose van de eerste week (C5); is de eerste week afgesloten (D2=B5) dan is de cumulatieve prognose gelijk aan de (cumulatieve) realisatie (F5; is gelijk aan D5) en anders doet de cum. prognose er niet toe en maken we die gelijk aan 0.
3. de cumulatieve prognose van de tweede week komt in cel E6:
   =ALS(B6=$D$2;F6;ALS(B6>$D$2;E5+C6;0))
   Als het de laatst gerealiseerde week betreft (B6=$D$2) dan komt hier de waarde van de cumulatieve realisatie (F6). Als het weeknummer groter is dan de afgesloten week (B6>$D$2)dan is de cumulatieve prognose gelijk aan de vorige (E5) plus de prognose van deze week (C6) en anders doet de prognose er niet meer toe (dus 0).
4. de formule in E6 kan naar beneden gekopieerd worden (vandaar dat D2 ‘absoluut’ is gemaakt mbv de $-tekens).
5. nu nog de cumulatieve realisatie: in cel F5 komt de formule
   =ALS($D$2>=B5;D5;0)
   Dus als de gerealiseerde week (D2) groter of gelijk is aan de eerste week (B5) dan wordt de eerste cumulatieve realisatie gelijk aan de eerste realisatie (D5) en anders 0.
6. in F6 komt de tweede cumulatieve realisatie:
   =ALS($D$2>=B6;F5+D6;0)
   Als de gerealiseerde week (D2) groter of gelijk is aan de betreffende week (B6) dan wordt de cumulatieve realisatie gelijk aan de vorige cumulatiieve realisatie (F5) plus de realisatie van deze week (D6) en anders 0.
7. ook deze formule kan naar beneden worden gekopieerd.

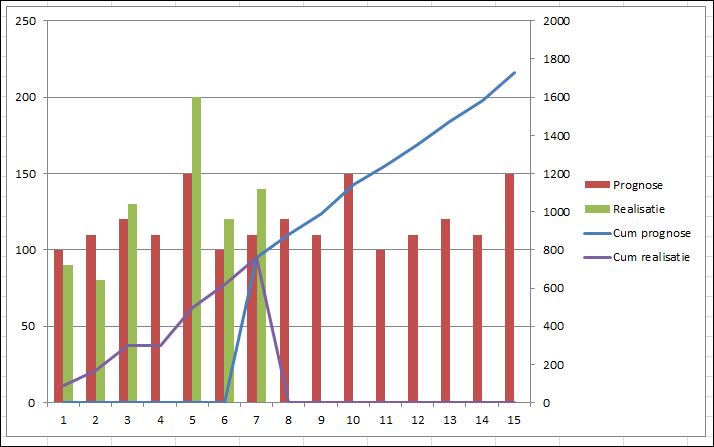De bijbehorende grafiek laat het resultaat zien, wanneer de realisatie van week 7 bekend is (de weekcijfers horen bij de linker (primaire) as, de cumulatieven bij de rechter (secundaire) as).

Hier wordt het probleem van Hasan zichtbaar: door de nullen in de diverse formules zien we een vreemde overgang van week 6 naar 7 (bij de cumulatieve prognose) en van week 7 naar 8 (bij de realisatie). Ook het wijzigen van de 0 in de formules in dubbele aanhalingstekens levert geen oplossing; Excel interpreteert dit in de grafiek als nul-waarden.

Prognose versus realisatie, grafiek zonder nullen

De enige oplossing (die ik kan bedenken) is om de nullen niet te vervangen door iets leegs (de dubbele aanhalingstekens) maar door de functie NB(). Deze geeft aan dat de waarde Niet Bekend is en deze worden in de grafiek niet weergegeven (zie tabblad Cum3 in het Voorbeeldbestand).

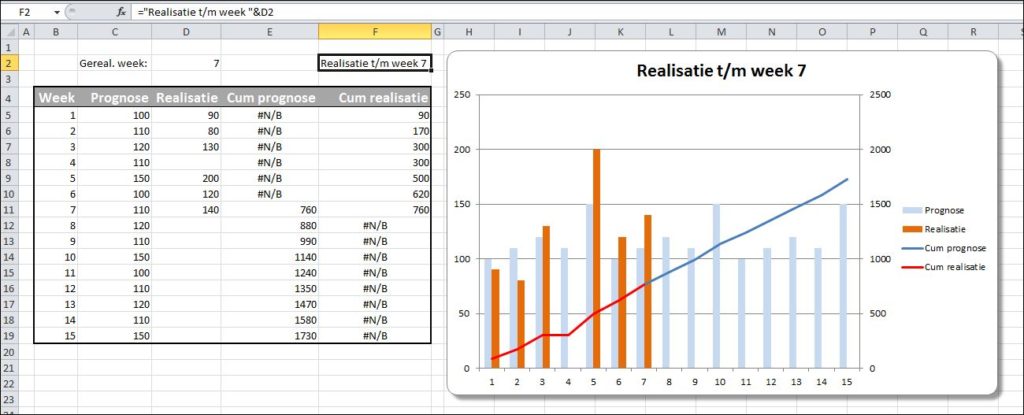
Dat ziet er beter uit:

1. De cumulatieve lijn loopt netjes door.
2. De grafiek heeft een dynamische titel; gekoppeld aan cel F2.
3. Kleuren zijn aan elkaar aangepast.
4. De secundaire as heeft een zodanige vaste verdeling gekregen (een maximum van 2500), dat de horizontale lijnen én links én rechts toegepast kunnen worden.

NB Is niet alleen de grafiek van belang maar wordt ook de tabel gebruikt in rapportages, zorg dan dat de #N/B’s niet zichtbaar zijn; dat kan eenvoudig met een voorwaardelijke opmaak.