Het vorige artikel ging over Voorspellen.
We hebben daar laten zien hoe je op diverse manieren op basis van historische gegevens iets kunt zeggen over de toekomst.
Dat daarbij veel ‘slagen om de arm’ gehouden moeten worden, mag duidelijk zijn: als er ook maar iets in de omgevingsfactoren verandert, kunnen de voorspellingen ver afwijken van de nog te behalen resultaten.
In dit artikel gaan we de zaak omdraaien: op basis van feiten/metingen én scenario’s voor omgevingsfactoren berekenen we de consequenties voor de toekomstige resultaten.
Als voorbeeld voor de werkwijze kijken we of we de waterstanden in de Geul (het gedeelte vanaf de bron tot aan Valkenburg) op deze manier zouden kunnen voorspellen.
Alvast een disclaimer: het is nog een heel eenvoudig model, dus ik blijf nog even, 75 meter hoger, in Heerlen wonen!
In dit voorbeeld wordt gebruik gemaakt van enkele (minder bekende) Excel-technieken: kruispunt van reeksen en het toepassen van een zelf-gedefinieerde kansverdeling.
Probleem-beschrijving
Zoals gezegd gaan we het probleem flink versimpelen zodat we het in een eenvoudig model kunnen gebruiken (zie het tabblad Data van het Voorbeeldbestand):
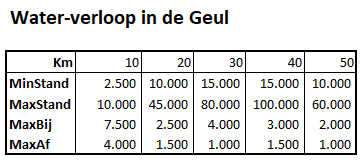
- vanaf de bron slingert de Geul zich over ongeveer 50km naar Valkenburg
- dit gedeelte van de rivier wordt in 5 gelijke delen verdeeld
- per deel ligt vast hoeveel water er altijd blijft staan (MinStand).
Vanaf de bron is de rivier gemiddeld 1m breed en er staat altijd minimaal 25cm water, dus dat is 2.500m3.
In Valkenburg is de rivier maar 2m breed, maar is altijd minstens 50cm diep. - ook leggen we de hoeveelheid water vast (MaxStand) waarbij het gebied gaat overstromen.
Vanaf de bron neemt deze maximale stand toe; net voor Valkenburg heeft de rivier de ruimte in de breedte, maar in het stadje wordt die over een flink stuk ingeperkt tot 2m. - door regenval komt er water bij. Per deel ramen we de maximale hoeveelheid water dat daar per dag in de rivier terecht komt (MaxBij).
- als laatste hebben we nog nodig hoeveel water er dagelijks maximaal afgevoerd kan worden (MaxAf; vaak beperkt door het meanderen, versmallingen etcetera).
NB nog maar een keer: dit zijn heel simpele benaderingen; om het model te verbeteren zouden exactere metingen moeten worden uitgevoerd.
Kruispunt
Voordat we het eerste model gaan bekijken bespreken we eerst een Excel-techniek die in dat model gebruikt zal worden.
In het overzicht op het tabblad Data hebben diverse reeksen een naam gekregen: de gegevens achter MinStand, MaxStand et cetera krijgen de naam uit de eerste kolom.
Voor de kolommen zouden we ook zoiets willen doen, maar de kolomkoppen bestaan uitsluitend uit getallen en Excel-namen moeten beginnen met een letter of speciaal teken. Ook één of twee letters er voor zetten is niet voldoende omdat er dan een verwijzing naar een kolomnaam ontstaat. We hebben er voor gekozen om de gegevens in de kolommen de naam _Km10, _Km20 et cetera te geven.
Om in een tabel gegevens op te zoeken gebruiken we vaak Vert.Zoeken of een combinatie van Index en Vergelijken.
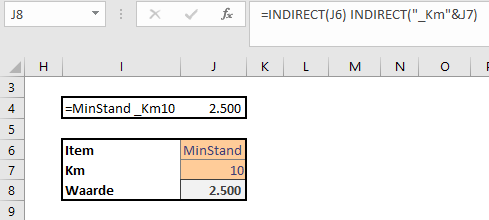
In het Voorbeeldbestand gebruiken we de kruispunt-techniek: in cel J4 van het tabblad Data staat de formule
=MinStand _Km10.
LET OP de 2 namen moeten gescheiden zijn door een spatie.
Het resultaat van de formule is de inhoud van de cel op het kruispunt van de 2 reeksen.
We kunnen de formule dynamisch maken: in plaats van harde namen, willen we verwijzingen naar cellen gebruiken. Helaas: een gewone verwijzing werkt niet, we moeten de functie Indirect gebruiken (zie de formule in cel J8:
=INDIRECT(J6) INDIRECT(“_Km”&J7)). Plaats wel een spatie tussen de 2 Indirect-functies!
Eerste model
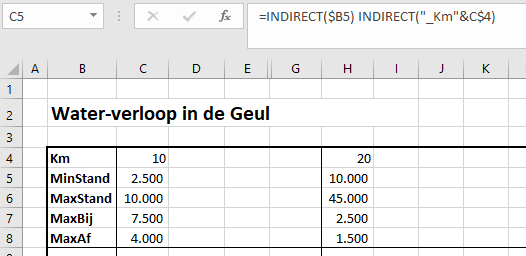
Op het tabblad Simpel van het Voorbeeldbestand nemen we allereerst met de kruispunt-techniek de gegevens uit het tabblad Data over. Door een juiste mix van absolute en relatieve verwijzingen kan de formule uit cel C5 overal gekopieerd worden.
Om te voorkomen dat per ongeluk basis-gegevens worden overschreven zijn de model-tabbladen beveiligd (wel zonder wachtwoord).
Wil je gegevens wijzigen, doe dat dan in het tabblad Data.
De opbouw van het model:
- we gaan ervanuit dat op dag 1 de rivier overal de minimumstand heeft.
- in de kolom daarnaast bepalen we de hoeveelheid water die er bij komt, door een willekeurig getal te kiezen tussen 0 en MaxBij voor dat deel van de rivier.
- de hoeveelheid water, dat wordt afgevoerd, wordt bepaald door de formule (in cel E11)
=ALS(C11+D11>C$5;MIN(C$8;C11+D11-C$5);0)
Dus als de beginstand plus het water, dat er bij komt, meer is dan de minimumstand dan wordt er water afgevoerd, anders niets. De afvoer is gelijk aan de beginstand plus de toevoer minus de minimale stand. Maar als daarmee de MaxAf wordt overschreden, dan wordt de MaxAf afgevoerd. - de berekening van de eindstand (in cel G11) is dan makkelijk: =C11+D11-E11
- de beginstand van de volgende dag is de eindstand van de dag er voor. De berekening van de overige gegevens van die dag is gelijk aan die van de eerste dag.
- bij de volgende delen van de rivier is de berekening precies hetzelfde met één verschil: de hoeveelheid water dat er per dag bij komt is niet alleen de hoeveelheid regen maar ook de hoeveelheid die uit het vorige deel van de rivier komt (kolom Af).
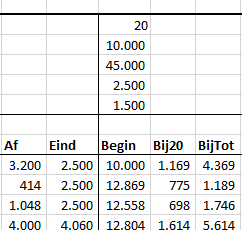
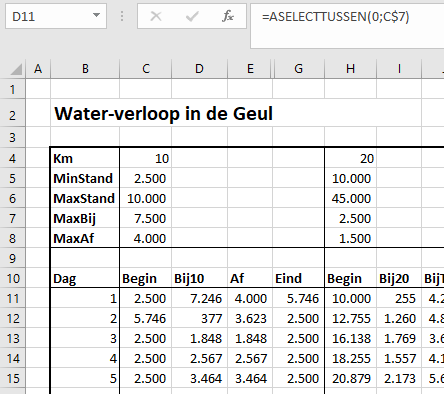
Zo gaat het resultaat er dan uitzien (zie het tabblad Simpel van het Voorbeeldbestand):
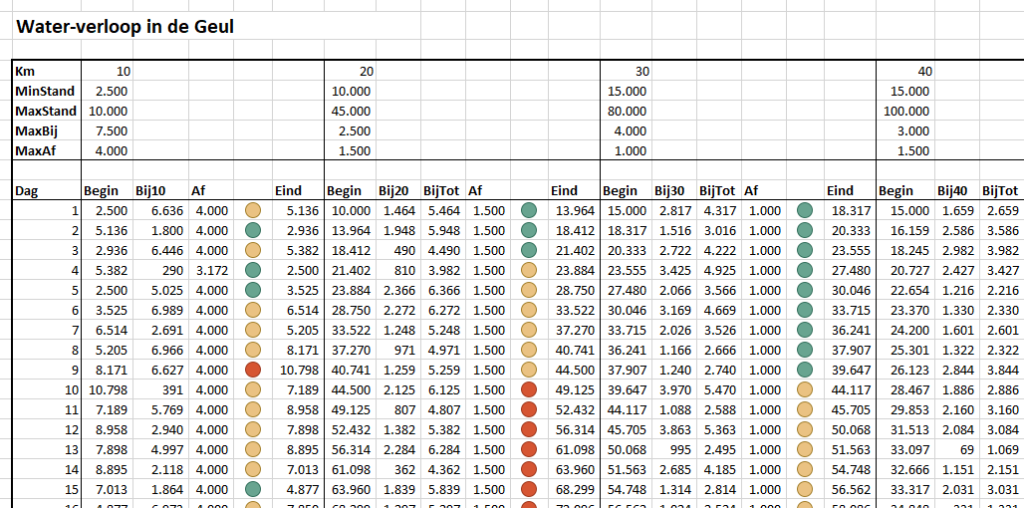
Om snel te zien of de eindstanden per dag nog ‘behapbaar’ zijn, zijn er kolommen tussengevoegd met een voorwaardelijke opmaak (stoplichtmodel).
Druk op F9 (herberekenen) en u ziet wat de consequenties volgens dit model zijn voor de waterstromen in de Geul. Vanwege de willekeurige hoeveelheid regen, die gegenereerd wordt, wijzigen iedere keer alle resultaten. Hou F9 vast en u ziet snel waar de grootste problemen worden verwacht.
Aangepast model
Eén van de gehanteerde aannames (los van de onderliggende ‘metingen’) rammelt nogal: als het in één deel hard regent, dan kan het in het volgende deel bijna droog zijn. Dat is natuurlijk op zo’n korte afstand helemaal niet reëel.
Op het tabblad Afh van het Voorbeeldbestand vindt u dan ook een ander model. Daarbij krijgt het eerste deel van de rivier per dag nog steeds een willekeurige hoeveelheid regen, maar de andere delen krijgen op die dag een evenredige hoeveelheid.
In cel I11 staat daartoe de formule: =H$7*D11/C$7
De maximaal verwachte regen in het tweede deel (H7) wordt vermenigvuldigd met de hoeveelheid regen in het eerste deel (D11) gedeeld door de maximaal verwachte regen in het tweede deel (C7) .
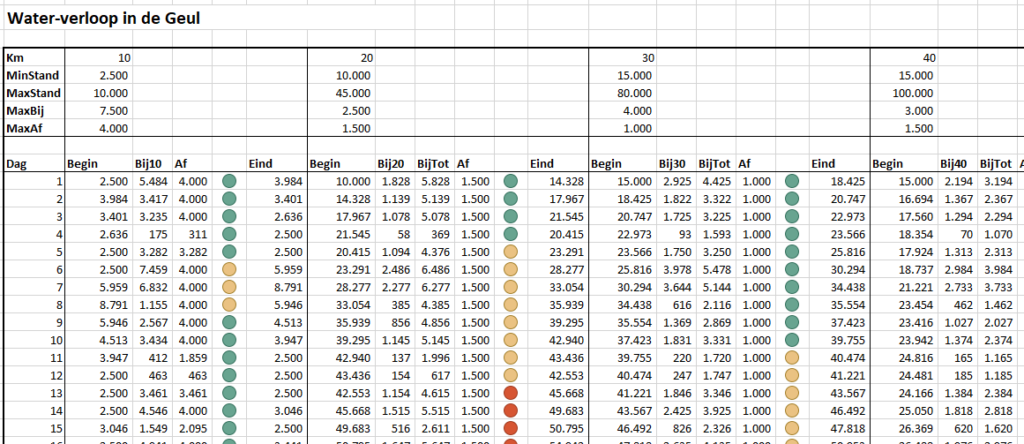
Ook nu ontstaan in het tweede gedeelte van de rivier al snel overstromingen.
Eigen kansverdeling
Bij de vorige modellen hebben we gebruik gemaakt van een zogenaamde discrete, uniforme verdeling (iedere hoeveelheid regen heeft even veel kans om voor te komen).
Een andere bekende verdeling is de normale distributie.
Maar allebei geven ze niet goed weer hoe de regen zich gedraagt in onze regio.
De kans dat het op een dag niet regent is (gelukkig) groter dan alle andere mogelijkheden. Maar als het regent dan komt er ook echt wel wat naar beneden.
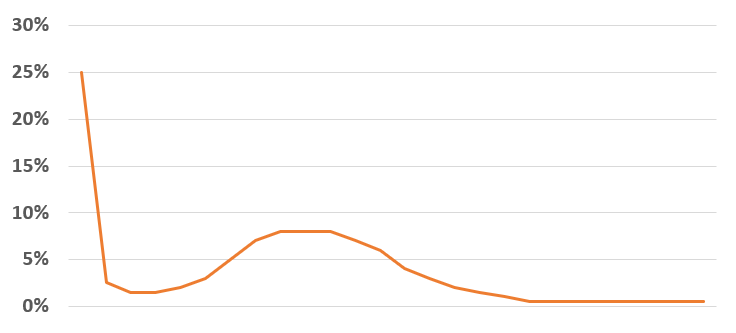
De volgende verdeling geeft dat idee weer:
De kans dat het niet regent is in dit voorbeeld 25%, kans op een heel klein beetje regen is klein, de kans op iets meer regen wordt groter en de kans op heel veel regen is heel klein. Deze verdeling zouden we in ons model willen gebruiken.
Voordat we dat doen, kijken we even gedetailleerder naar deze verdeling.
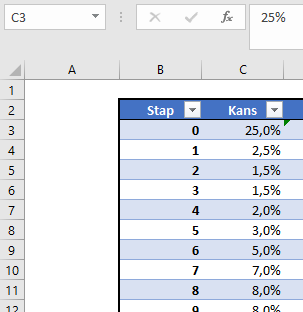
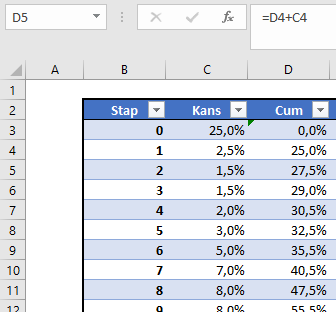
In het tabblad KansVerdeling van het Voorbeeldbestand is de gewenste verdeling ‘met de hand’ ingevuld. Stap 0 krijgt een kans van 25%, de volgende stap 2,5%, dan 1,5% et cetera tot en met stap 25 die een kans van 0,5% heeft.
De tabel (met de naam Tabel1) heeft ook nog een cumulatieve kolom.
LET OP in deze kolom staan de cumulatieven tot en met de VORIGE stap!
We gaan deze tabel gebruiken om vanuit een percentage in de cumulatieve kolom de daarbij behorende stap op te zoeken. Een combinatie van de functies Index en Vergelijken levert het gewenste resultaat: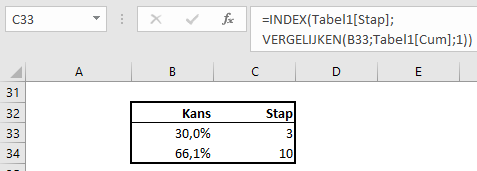
NB de 3e parameter in de functie Vergelijken heeft de waarde 1. De functie zoekt dan naar de grootste waarde die kleiner dan of gelijk is aan de Zoekwaarde (de eerste parameter).
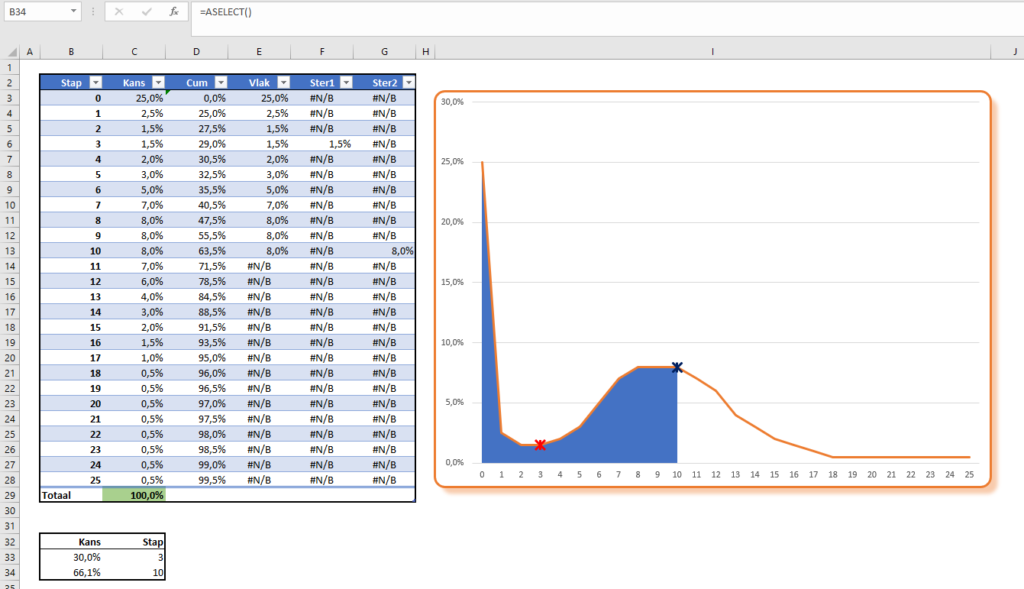
Druk op F9 om in B34 een andere kans te genereren.
Met deze techniek vertalen we een continue, uniforme distributie naar een discrete, gewenste verdeling. 25% van de willekeurige getallen in cel B34 laten in cel C34 een stap=0 zien, 2,5% genereren een stap=1, 1,5% een stap=2 enzovoort.
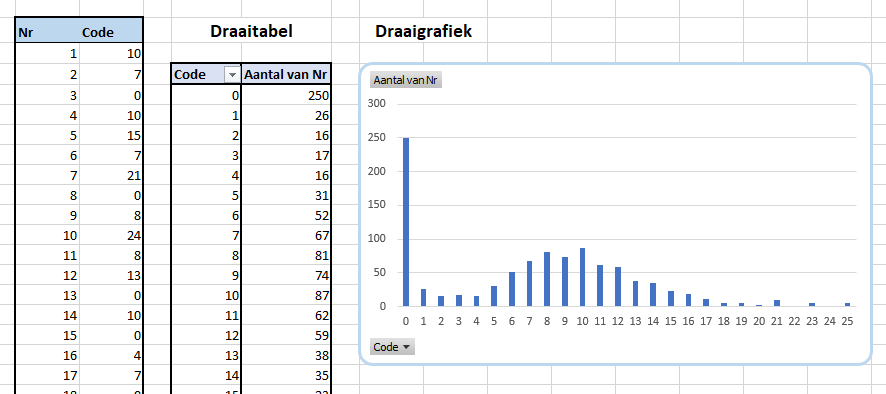
Ter controle worden in het tabblad VerdContr telkens 1.000 percentages gegeneerd, die op bovenstaande manier naar een Code worden vertaald. Wanneer deze codes in een draaitabel worden gezet, kunnen we daarop een draaigrafiek baseren. We zien dan onze gewenste verdeling terug.
NB Vernieuw de draaitabel en alles wijzigt. Aangezien Excel automatisch alles opnieuw berekent (en dus ook nieuwe kansen bepaalt) hoeven we niet meer op F9 te drukken om nieuwe codes te krijgen.
Laatste model
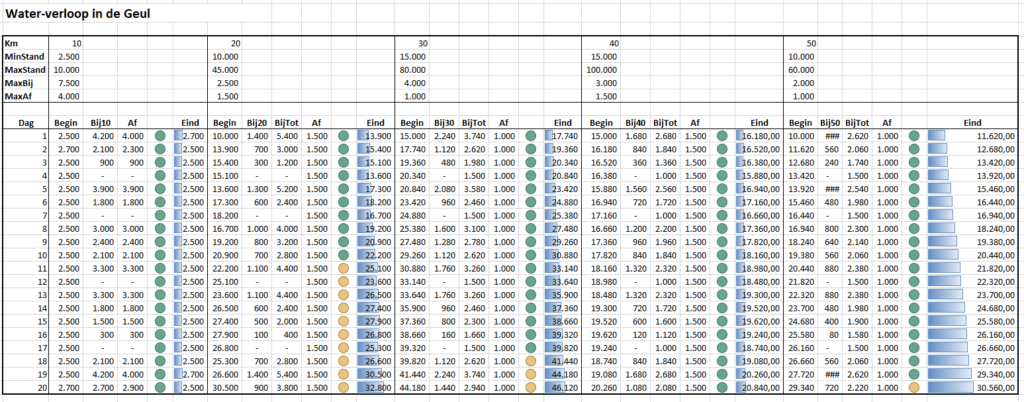
In het tabblad Verdeling van het Voorbeeldbestand hebben we bovenstaande verdeling en techniek gebruikt om het model te verbeteren. In de Bij-kolom in het 10-km-deel van de Geul gebruiken we de formule:
=INDEX(Tabel1[Stap];VERGELIJKEN(ASELECT();Tabel1[Cum];1))*C$7/MAX(Tabel1[Stap])
Dus de gevonden stap wordt geschaald naar een waarde tussen 0 en de maximaal verwachte regenval.
NB1 je kunt de gewenste verdeling verfijnen door meer stappen in te voegen; door MAX(Tabel1[Stap]) wordt de gevonden stap op de juiste manier gecorrigeerd.
Zorg wel dat de som van de kansen in de gewenste verdeling precies 100% is.
NB2 aan de Eind-kolommen is nog een voorwaardelijke opmaak toegevoegd waardoor de ‘waterstand’ snel kan worden ingeschat.
Allerlaatste model
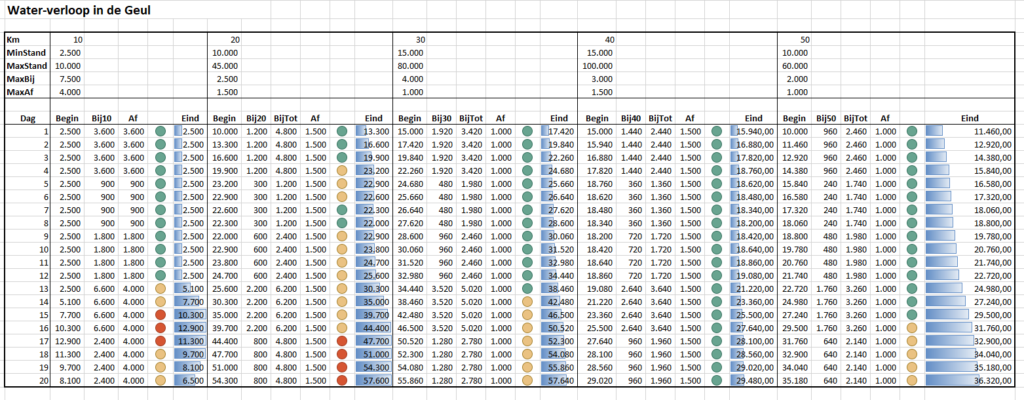
In het vorige model kan de hoeveelheid regen van dag op dag flink fluctueren; dat is natuurlijk niet helemaal de realiteit. In het tabblad Verdeling4gelijk van het Voorbeeldbestand hebben we er voor gezorgd dat er telkens 4 dagen op een rij ‘hetzelfde weer’ is, beter gezegd dat het telkens 4 dagen even veel regent.
En zo kunnen we nog wel even doorgaan. Iedere aanpassing aan het model roept weer vragen op en nodigt uit tot nieuwe aanpassingen. Wat te denken van de continue toename van het water in Valkenburg. Hoe zal de situatie daar zijn na 40 dagen???? Ergens zit nog iets geks in het model.
Maar goed, we laten de verdere verfijning over aan Rijkswaterstaat 😉