Iedereen maakt het wel eens mee dat Excel ineens een melding geeft dat er een Kringverwijzing is gesignaleerd.
Wat betekent dat? Hoe weet je of er Kringverwijzingen zijn? Hoe los je het op? En kunnen we kringverwijzingen zinvol toepassen in de praktijk? Om de laatste vraag alvast te beantwoorden: jazeker, en dat noemen we dan Iteraties.
Kringverwijzing
Soms gebeurt het ineens: ben je ijverig bezig een mooie spreadsheet in elkaar te zetten, krijg je ineens de volgende melding:

Deze melding kun je ook krijgen als je een bestaande spreadsheet opent.
De uitleg in de melding maakt wel duidelijk wat er aan de hand is: een formule in een cel verwijst naar deze cel zelf (direct of indirect). Excel weet dan niet wat ie moet doen: 1 keer berekenen of, als dat resultaat is berekend, nog een keer? En daarna nog een keer? In de standaard-instelling (waarbij Excel alles automatisch herberekent) stopt de berekening en is het resultaat van de formule gelijk aan 0.
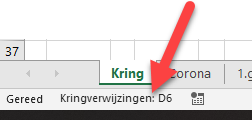
Wanneer Excel een kringverwijzing tegenkomt dan wordt dit zichtbaar in de status-balk onder aan het Excel-venster.
LET OP1 ook al staat er in de statusbalk maar één cel, er kunnen meerdere kringverwijzingen in het spreadsheet voorkomen.
LET OP2 als er kringverwijzingen zijn dan moet je normaal gesproken deze direct oplossen; ALLE resultaten van berekeningen zijn daardoor onbetrouwbaar.
Een paar voorbeelden (zie het tabblad Kring van het Voorbeeldbestand):
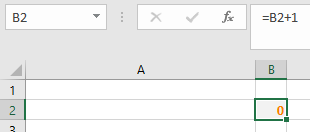
In cel B2 staat de formule =B2+1.
Er staat nu de waarde 0, dus het resultaat zou dan 1 moeten zijn. Maar als er 1 staat in de cel, dan wordt het resultaat van de formule 2 enzovoort.
Meestal betekent dit dat er naar een verkeerde cel wordt verwezen of dat de formule in de verkeerde cel wordt geplaatst.
De oplossing is simpel: pas de verwijzing in de formule aan of verplaats de formule.
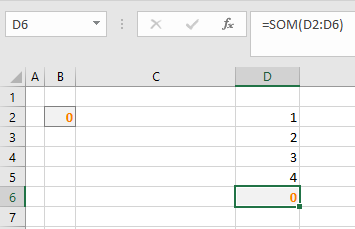
Een vaker voorkomende fout bij het maken van een spreadsheet: in de verwijzing in een Som-formule wordt ook verwezen naar de cel, waarin de formule staat (in het voorbeeld hiernaast D6).
Oplossing: zorg dat de verwijzing in de formule naar de juiste cellen verwijst.
We kennen ook een zogenaamde verborgen kringverwijzing; deze zijn soms moeilijker op te sporen omdat deze niet altijd optreden.
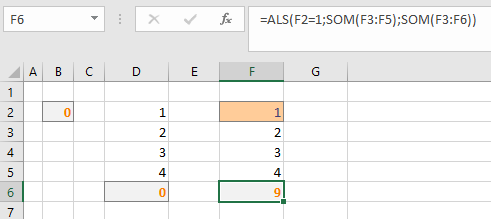
In het voorbeeld hiernaast staat in cel F6 een formule die afhankelijk van de waarde in F2 twee verschillende berekeningen uitvoert.
Als F2 de waarde 1 bevat kan Excel de berekening gewoon uitvoeren en zal dan ook niets melden; bevat die cel echter een andere waarde dan wordt de tweede berekening uitgevoerd en dan ontstaat er wel een kringverwijzing.
Oplossing: zorg dat de verwijzing in de formule naar de juiste cellen verwijst.
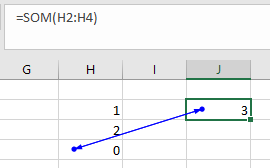
Een voorbeeld van een indirecte kringverwijzing: in cel J2 staat een verwijzing naar de cellen H2:H4. Niets geks.
Behalve als we kijken naar de inhoud van cel H4: =SOM(H2:J3), dus hierbij wordt ook impliciet verwezen naar de cel J2.
Dit soort fouten zijn vaak moeilijker te achterhalen. Maar gelukkig helpt Excel ons door een lijntje tussen de 2 cellen te tekenen. Dubbelklik hierop en Excel toont afwisselend de inhoud van de 2 betrokken cellen.
Toepassing Kringverwijzing
Zoals gezegd: meestal duidt het optreden van kringverwijzingen er op, dat er ergens in één of meer formules fouten staan. Maar soms wil je bewust gebruik maken van dit fenomeen.
Eigenlijk overal waar een eindstand van een periode weer gebruikt wordt als input voor de berekeningen in de volgende periode zouden we kringverwijzingen kunnen tegenkomen/gebruiken.
Bijvoorbeeld wanneer we het verloop van een hypotheek in de tijd willen berekenen, zullen we de schuldrest op het einde van de maand gebruiken om de rente en aflossing van de volgende maand te berekenen. Daardoor kennen we weer de schuldrest op het einde van die periode . Deze gebruiken we dan weer als input voor de volgende maand etc.
Een simpeler voorbeeld staat op het tabblad Corona van het Voorbeeldbestand .
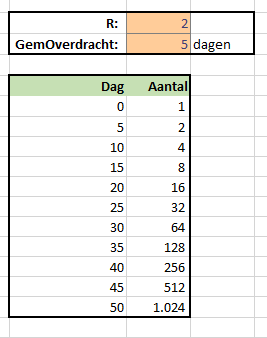
De berekening kent twee input-variabelen: de zogenaamde R en het gemiddeld aantal dagen dat het duurt om een besmetting over te dragen.
Bij een R=2 en het aantal dagen=5 ligt, wanneer we op dag 0 met 1 besmetting starten, na 50 dagen het daaruit voorkomende aantal besmettingen al boven de 1.000.
In dit flink versimpelde model bepalen we het aantal besmettingen op het einde van een periode door de stand van de vorige periode te vermenigvuldigen met R.
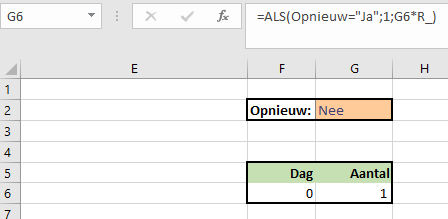
Als we niet geïnteresseerd zijn in de tussenresultaten zouden we het eindresultaat (in het voorbeeld in cel G6) ook kunnen berekenen door het het vorige resultaat in die cel te vermenigvuldigen met de R-waarde.
Helaas: Excel voert die berekening normaal gesproken niet uit, want er ontstaat daar een kringverwijzing (zie op de statusbalk linksonder). En als die het wel zou kunnen/willen berekenen: wanneer moet die stoppen? Na 10 keer zoals in de berekening hiervoor of na 20 of na ???
NB1 in cel F6 staat de berekening =F6+GemOvDgn, dus ook daar ontstaat een kringverwijzing.
NB2 er ontstaan geen kringverwijzingen wanneer Opnieuw (de waarde in cel G2) gelijk is aan Ja. Dit gebruiken we om ons model op een standaard-waarde in te stellen (zie hierna).
We gaan de Excel-omgeving aanpassen zodat we de berekening in G6 WEL kunnen uitvoeren:
- kies in de menutab Bestand de button Opties

- klik op Formules en vul de Berekeningsopties in zoals hieronder, dus op handmatig berekenen en Iteratieve berekeningen inschakelen:
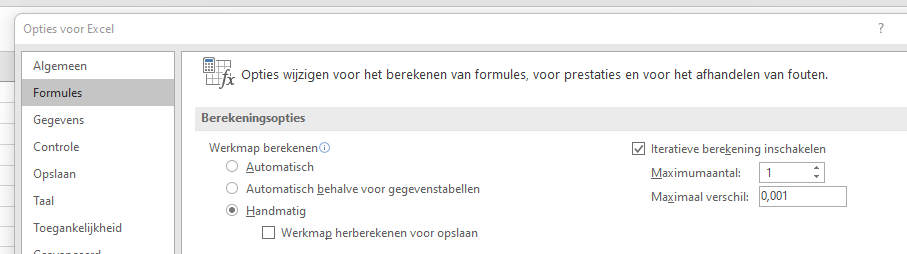
- klik op OK
Nu kunnen we gaan rekenen:
- vul cel G2 met de waarde Ja
- we hebben Excel op Handmatig berekenen gezet, dus druk op F9 of klik onderaan in de statusbalk op Berekenen
- geef cel G2 de waarde Nee
- en kies opnieuw Berekenen:
- telkens wanneer we herberekenen, verandert het resultaat:
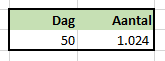
- wil je opnieuw beginnen? Vul cel G2 met de waarde Ja, wijzig eventueel de R en het aantal dagen in kolom C, vul G2 met Nee en kies Herberekenen zoals in stap 2.
NB in de Berekeningsopties hebben we het aantal Iteraties op 1 gezet. Iedere keer wanneer we herberekenen, gaat Excel dus alle cellen één keer langs om formules in die cellen te berekenen. Zet je het aantal Iteraties hoger dan voert Excel de berekeningen dat aantal keren achter elkaar uit.
LET OP vergeet niet de Berekeningsopties weer op Automatisch berekenen te zetten wanneer je met een ander spreadsheet aan de slag gaat!
Game of life
Het vorige voorbeeld laat goed de werking van Kruisverwijzingen/Iteraties zien. Een ander bekend (en zinvoller) voorbeeld is Conway’s Game of Life.
De Britse wiskundige Conway bedacht dit ‘spel’ in 1970 om de groei van een organisme na te bootsen, gebaseerd op het werk van John von Neumann.
In een 2-dimensionaal rooster heeft iedere cel óf de waarde Bewoond óf de waarde Onbewoond. Voor elke levenscyclus is iedere cel afhankelijk van de status van zijn 8 buren:
- iedere bewoonde cel met minder dan 2 bewoonde buren sterft (onderbevolking)
- iedere bewoonde cel met 2 of 3 bewoonde buren blijft bewoond
- iedere bewoonde cel met meer dan 3 bewoonde buren sterft (overbevolking)
- iedere onbewoonde cel met precies 3 bewoonde buren wordt bewoond (reproductie)
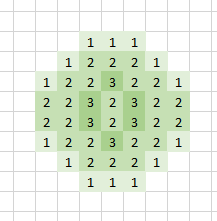
Hiernaast zie je de ‘vertaling’ van een patroon naar het aantal buren.
Onderstaande uitwerking van de Game of Life in Excel is gebaseerd op een artikel uit 2007: www.microsoft.com/…./iteration-conways-game-of-life/
Om het ‘levenspel’ in Excel te implementeren maken we de volgende afspraken:
- voor het Conway-rooster gebruiken we natuurlijk het raster van een tabblad
- waar Conway een oneindig groot rooster gebruikt, beperken we ons tot 30 rijen en 40 kolommen
- in een ‘bewoonde’ cel plaatsen we een 1, anders een 0
- via Voorwaardelijke opmaak vullen we een bewoonde cel met een groene kleur, anders wordt de cel wit
Om iedere levenssstap na te bootsen vertalen we de Conway-regels in een formule:
- eerst als een cel bewoond is: als het aantal bewoonde buren 0 of 1 is dan wordt de cel 0, als dat aantal 2 of 3 is dan blijft de cel 1, anders wordt de cel 0. In een Excel-formule: KIEZEN(buren+1);0;0;1;1;0;0;0;0;0)
NB de laagste waarde van de eerste parameter moet 1 zijn, dus we verhogen het aantal buren met 1.
Iets compacter: KIEZEN(MIN(5;buren+1));0;0;1;1;0) - als we te maken hebben met een onbewoonde cel: ALS(buren=3;1;0)
Gecombineerd: ALS(celwaarde=1;KIEZEN(MIN(5;.buren+1);0;0;1;1;0);ALS(buren=3;1;0))
In het tabblad 1.Game van het Voorbeeldbestand staat een implementatie van het spel.
De bewoonde buren van een cel liggen vast in een ander tabblad (2.Buren).
Het aantal bewoonde buren van bijvoorbeeld cel E6 in het tabblad 1.Game liggen vast in cel E6 van het tabblad 2.Buren.
De gecombineerde formule hierboven wordt dan voor cel E6: =ALS(E6=1;KIEZEN(MIN(5;.’2.Buren’!E6+1);0;0;1;1;0);ALS(‘2.Buren’!E6=3;1;0))
Nu zijn we er bijna: we moeten ook nog een start-situatie kunnen vastleggen.
Cel C2 (met de naam Reset) geven we een waarde WAAR als we het rooster in de begin-situatie willen krijgen; we passen daarom de formules in het rooster aan:
=ALS(Reset;Basis!E6;ALS(E6=1;KIEZEN(MIN(5;’2.Buren’!E6+1);0;0;1;1;0);ALS(‘2.Buren’!E6=3;1;0)))
en leggen de gewenste begin-situatie in het tabblad Basis vast.
NB1 om het systeem te resetten kun je ook een vinkje plaatsen in het hokje in kolom E; dit selectievakje is gekoppeld aan cel E2.
NB2 och ja, vergeet niet de Berekeningsopties aan te passen zoals hierboven beschreven en het spreadsheet handmatig te herberekenen door bijvoorbeeld F9 in te drukken.
NB3 cel C3 (met de naam Iteratie) bevat een teller voor het aantal uitgevoerde iteraties vanaf een reset: =ALS(Reset;0;Iteratie+1)
Voorbeeld-run (zorg dat de Berekeningsopties goed staan):
- vul de Reset-cel met de waarde WAAR (of vink het selectievakje aan)
- herbereken het spreadsheet (F9 of Berekenen in de statusbalk aanklikken)

- vul de Reset-cel met de waarde ONWAAR (of vink het selectievakje uit)
- herbereken het spreadsheet (F9 of Berekenen in de statusbalk aanklikken)
- herhaal stap 4 zo vaak als gewenst
 (dit is het resultaat na 6 iteraties)
(dit is het resultaat na 6 iteraties)
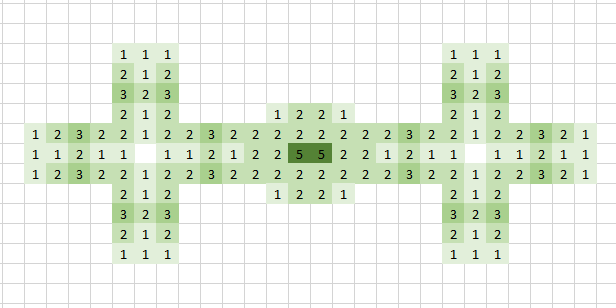
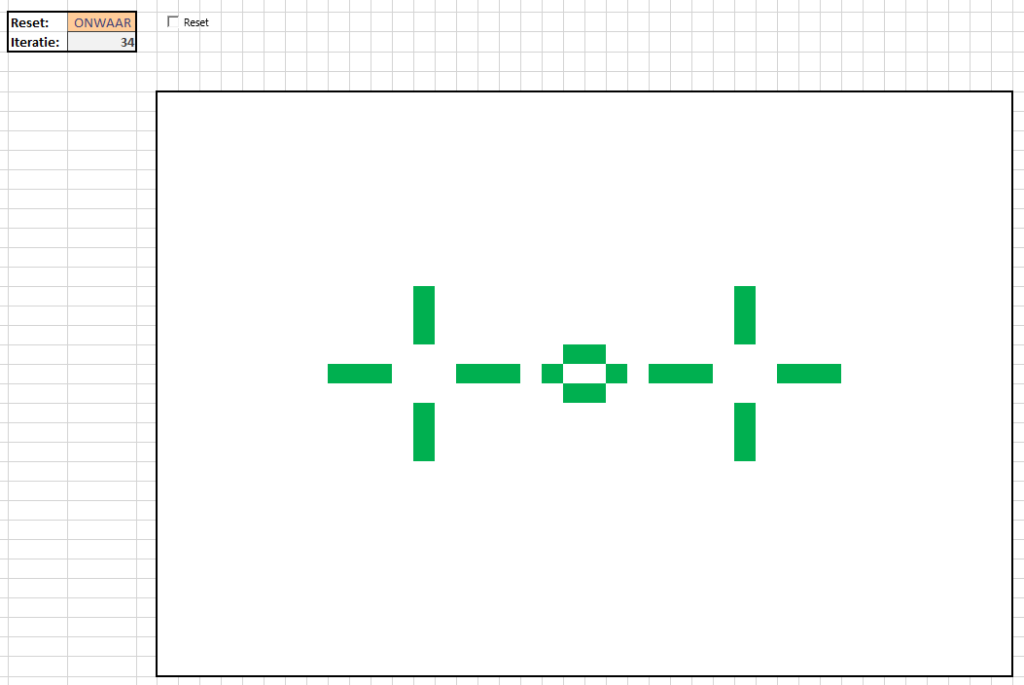
Na 13 iteraties ziet het scherm er zo uit: 
maar na 18 iteraties blijft een zogenaamde oscillator over: <–>
<–> 
NB1 dit voorbeeld eindigt in een 2-periode oscillator. Veel andere voorbeelden eindigen in een stabiele situatie (start bijvoorbeeld met een rijtje van 12 bewoonde cellen) of een leeg rooster (start met een rijtje van 6). Soms ontdek je een Life-game dat zich maar blijft ontwikkelen.
NB2 op internet zijn veel voorbeelden van dit spel te vinden (zie bijvoorbeeld en.wikipedia.org/wiki/…..Examples_of_patterns en playgameoflife.com).
NB3 Het rooster in het tabblad 1.Game (en alle anderen) is redelijk beperkt (30 x 40) maar voldoet voor de meeste bekende voorbeelden. Een mogelijke verbetering: pas op het tabblad 2.Buren de formules op de grenzen aan; vervang verwijzingen naar cellen buiten het rooster door verwijzingen naar cellen op de grens aan de andere kant van het rooster.
In het Voorbeeldbestand staan nog diverse tabbladen met mogelijke start-posities; de namen daarvan beginnen met Basis. Kopieer het rooster daaruit naar het tabblad Basis en herstart een run zoals hiervoor beschreven.
Wanneer je het tabblad Basis450 gebruikt zul je zien dat het heel lang duurt voordat er een stabiele situatie ontstaat. In dit soort gevallen is het handig om eerst het aantal iteraties per herberekeningsronde te verhogen in de Berekeningsopties: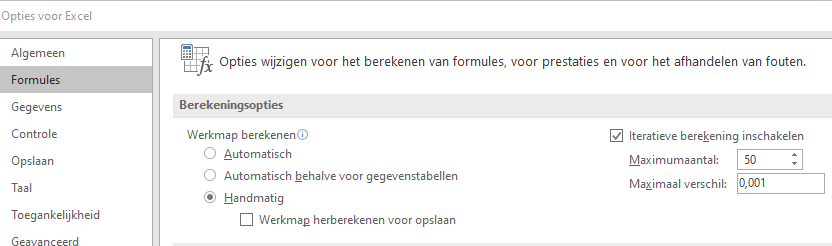
NB In dit systeem hebben we gebruik gemaakt van de volgende werking van Excel: het herberekenen van cellen begint op het eerste tabblad, daarna het tweede etc. Dus pas als alle berekeningen op het tabblad 1.Game zijn uitgevoerd, worden de cellen van het tabblad 2.Buren berekend.