LET OP: na het downloaden de extensie wijzigen in xlsb

De oudere jongeren onder ons (of de jongere ouderen?) weten het nog wel: in 1972 (50 jaar geleden) verscheen het Rapport van de Club van Rome met als ondertitel De grenzen aan de groei.
Een pocketboekje dat een intensieve discussie op gang heeft gebracht: voor sommige mensen was het een eye-opener (we kunnen niet blijven doorgaan met het ongelimiteerd opsouperen van onze hulpbronnen, we moeten ‘de groei’ temperen), anderen wezen er op dat je met het onderliggende model alles kunt bewijzen (een Eindhovense professor formuleerde dat als ‘Met dit model kun je ook je eigen handtekening maken; een kwestie van de parameters aanpassen aan je wensen‘).
In het vorige artikel van G-Info is een voorbeeld uit het rapport langs gekomen om te laten zien hoe je Vergelijkingen/formules in Excel kunt schrijven. Een losse opmerking daarbij (‘Zou het model in Excel nagebouwd kunnen worden?“) is het begin van een zoektocht geworden. Gelukkig kwam daarbij al snel een vereenvoudigd model naar boven. Het begin van een uitdaging: kan dit model in Excel op een zodanige manier geïmplementeerd worden, dat in ieder geval de resultaten van de Club van Rome gereproduceerd worden?
In dit artikel eerst een korte achtergrond van het Rapport van de Club van Rome, een uitleg van het vereenvoudigde model en daarna wat vingeroefeningen om te laten zien hoe we denken dat de implementatie er uit kan gaan zien.
Rapport van de Club van Rome
Wikipedia: “De grenzen aan de groei is een rapport van de Club van Rome uit 1972 waarin de uitputtingsproblematiek centraal staat. Het rapport werd uitgewerkt door een team van het Massachusetts Institute of Technology (MIT) onder leiding van Dennis Meadows en Donella Meadows. Het rapport heeft grote invloed gehad op het milieubewustzijn.
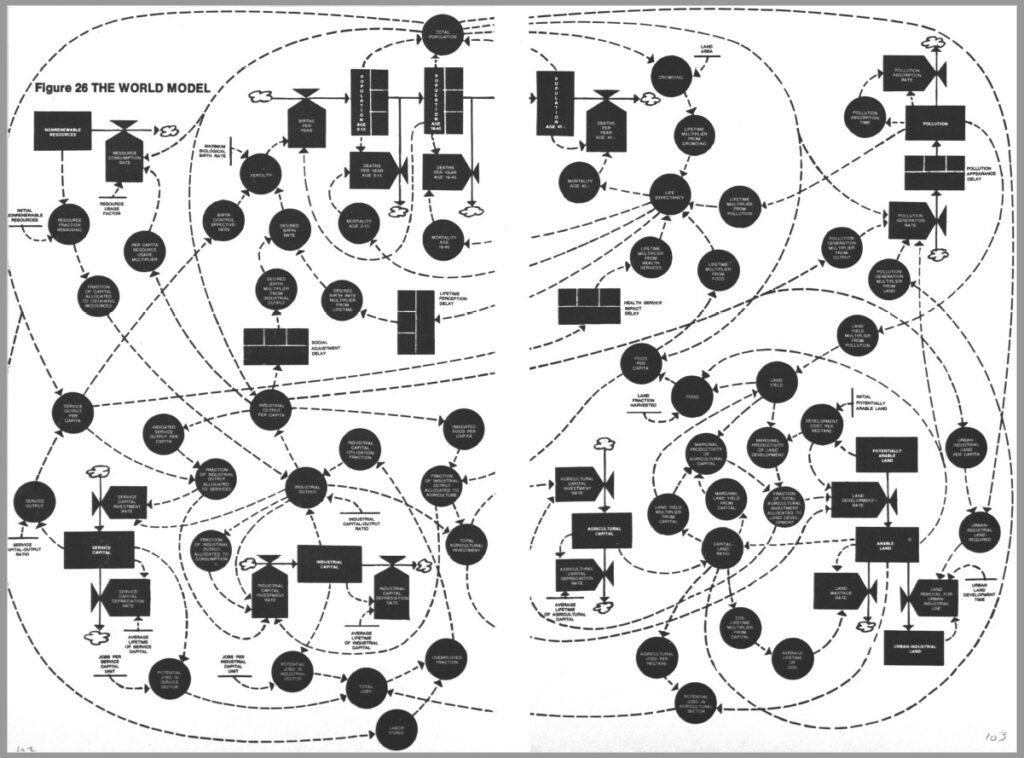
Aan de basis van de studie ligt het gebruik van een systeemdynamisch model met computersimulatie van interacties tussen bevolking, industriële groei, voedselproductie en limieten in de ecosystemen van de aarde: het World3-model, mede ontwikkeld door Jay Forrester. Van deze variabelen werd de ontwikkeling van 1900 tot 1970 vastgesteld. Vervolgens werden de trends voortgezet, waarbij verschillende aannames werden gedaan. Ervan uitgaande dat geen belangrijke veranderingen plaats zouden vinden in de fysieke, economische en sociale relaties (het referentie scenario) waren de uitkomsten schokkend. De natuurlijke hulpbronnen zouden gaandeweg uitgeput raken en de industriële groei remmen. De bevolkingsomvang en vervuiling zouden nog enige tijd toenemen, maar de verslechtering van de voedselvoorziening en de gezondheidszorg leidden in eerste instantie tot stilstand en later tot terugloop in de bevolkingsgroei.“
Het rapport was niet zozeer bedoeld om kwantitatieve voorspellingen over de toekomst te doen (de leden van de Club en MIT’ers beseften terdege dat het model daarvoor veel te globaal en simpel was). Het diende als input voor de discussie over de groei van de wereldbevolking, ons consumptiepatroon en het gebruik van de natuurlijke grondstoffen en het effect van milieuvervuiling.
Het model is doorgerekend met diverse scenario’s.
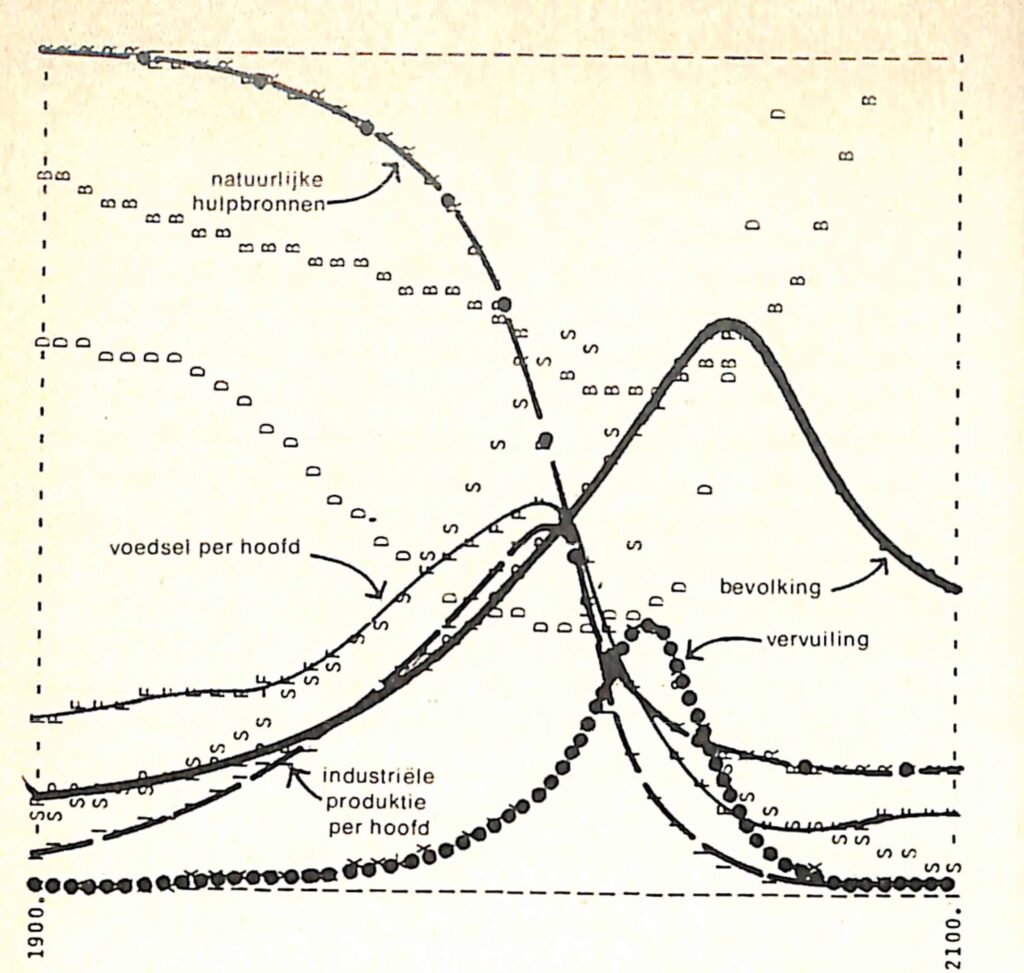
Hiernaast staat een grafische weergave van het resultaat van het standaard BAU-scenario (Bussiness As Usual). Daarin volgen alle variabelen van 1900 tot 1970 de historische waarden. De rest is door het model berekend op basis van de aanname dat “er geen belangrijke veranderingen plaatsvinden in de fysieke, economische of sociale relaties.“
De grafieken werden weergegeven door letters, waarna de belangrijkste variabelen met de hand werden ingetekend; B stelt het geboortecijfer voor, D het sterftecijfer en S de diensten per hoofd.
Uit het rapport: “Elk van de variabelen is uitgezet op een verschillende schaalverdeling. We hebben met opzet de verticale schaalverdelingen weggelaten en de horizontale tijdas geen indeling gegeven, omdat we de nadruk willen leggen op de algemene gedragspatronen, niet op de numerieke waarden die slechts onnauwkeurig bekend zijn. Maar de schalen zijn in alle scenario’s gelijk, zodat de grafieken gemakkelijk vergeleken kunnen worden.“
Iedereen die geïnteresseerd is in de resultaten van de scenario’s moeten we doorverwijzen naar diverse publicaties. De Nederlandstalige versie van het rapport is nog te koop, de Engelstalige versie is in PDF-versie te downloaden.
Het idee om eens te kijken of we met Excel het BAU-scenario zouden kunnen reproduceren, leek bij bestudering van deze info niet haalbaar. Totdat ….
Een vereenvoudigd model
Bij de zoektocht op internet kwam ik een studie tegen waarin de resultaten van het oorspronkelijke model vergeleken werden met recente data. Ook is daar een vereenvoudigd model te vinden.
Dit model bestaat uit 25 variabelen. Dat moet te doen zijn en ook het aantal verbanden daartussen lijkt behapbaar.
Misschien dat het toch gaat lukken om de resultaten uit 1972 te reproduceren! En dat dan niet alleen: misschien kunnen we de diverse parameters in het model zodanig aanpassen, dat we weten hoe we de wereld de juiste kant op kunnen sturen 😉
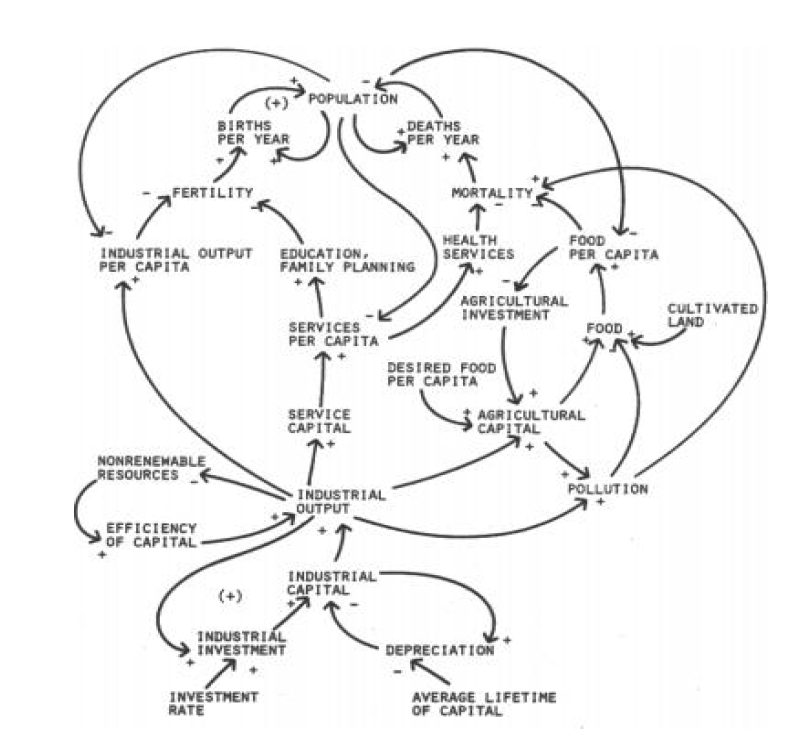
Op het tabblad SystemDynamics van het Voorbeeldbestand ziet u een aangepaste vorm van dit vereenvoudigde model:
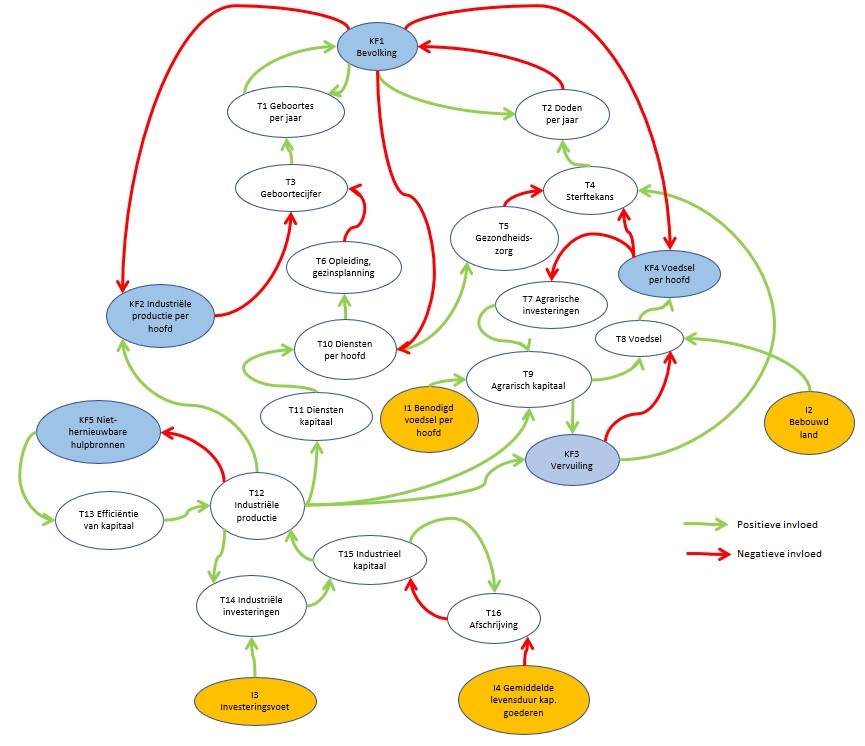
Bovenstaand model is in Excel gemaakt met 2 soorten vormen: Ovalen en Gekromde pijlen.
- Kies in de menutab Invoegen in het blok Illustraties de optie Vormen.
- Selecteer de gewenste vorm en ’teken’ met de muis ongeveer op de plaats waar deze moet komen.
- Pas in de menutab Hulpmiddelen voor tekenen de Opmaak aan.
- De ovalen zijn gemakkelijk groter en kleiner te maken door middel van de rondjes aan de zijkanten. Bovenin zit een greep waarmee de vorm gedraaid kan worden.
- De plaats en de vorm van de pijlen kunnen via de 3 bolletjes aangepast worden. Zorg wel dat de uiteinden van de pijl precies op één van de 8 rondjes van een ovaal terecht komen (het resultaat is dan een dicht zwart bolletje). Wanneer je achteraf een vorm verschuift zal de pijl meebewegen.
- Je kunt een tekst in een ovaal plaatsen door daarin te dubbel-klikken en dan de tekst te tikken.
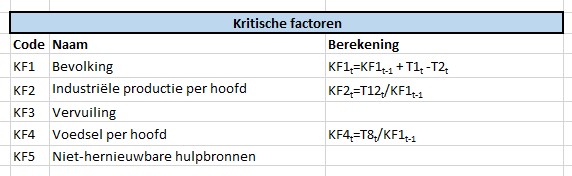
Om de consistentie te bewaken hebben we alle codes en namen in een apart tabblad Beschr vastgelegd. Door nu eenmaal in/op een ovaal te klikken kan in de formulebalk een verwijzing naar een cel in dit tabblad gemaakt worden.
De cellen in kolom D worden gebruikt in het model; afhankelijk van de grootte van de tekst plaatsen we tussen de Code en de Naam een spatie of een harde return (druk tussen de aanhalingstekens op Alt-Enter). Alle cellen in kolom D hebben een overeenkomende naam gekregen (bijvoorbeeld cel D4 heeft de naam KF1_; de underscore is nodig omdat Excel anders denkt dat we een verwijzing naar de cel in kolom KF en rij 1 bedoelen).
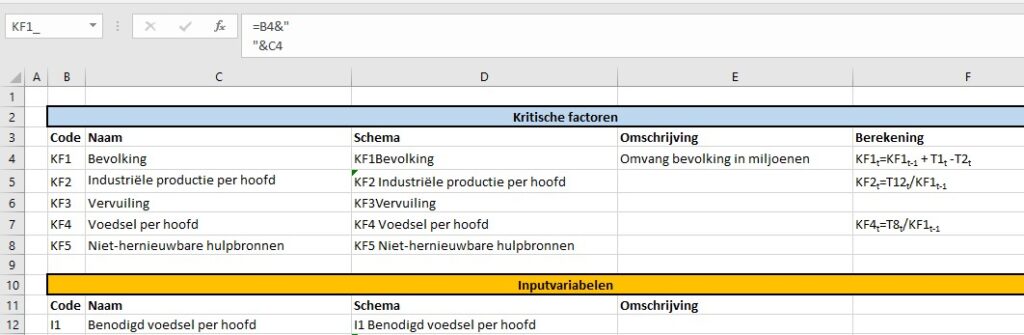
NB heb je een paar vormen (inclusief opmaak) die voldoen, dan kun je die natuurlijk ook kopiëren. De tekst (en misschien de grootte) aanpassen en je bent klaar.
Variabelen
We onderkennen in het model 3 soorten variabelen: de Inputs, de Kritische Factoren en de Tussen-variabelen. De Input-variabelen worden niet beïnvloed door de omgeving, maar kunnen wel in de loop van de jaren variëren. De KF’s zijn die 5 variabelen die in alle grafieken van het rapport terugkomen. Alle overige hebben de naam Tussen-variabelen gekregen.
Verbanden tussen variabelen
De pijlen in het model geven het verband tussen de diverse variabelen aan. De richting en kleur laten de soort beïnvloeding zien.
1. Lineair of absoluut verband
Tussen sommige variabelen zit een lineair/absoluut verband: variabelen worden bij elkaar opgeteld of op elkaar gedeeld om de waarde van een andere variabele te berekenen.
Bijvoorbeeld, voor de bevolkingsomvang gebruiken we de volgende formule:
KF1t=KF1t-1 + T1t -T2t
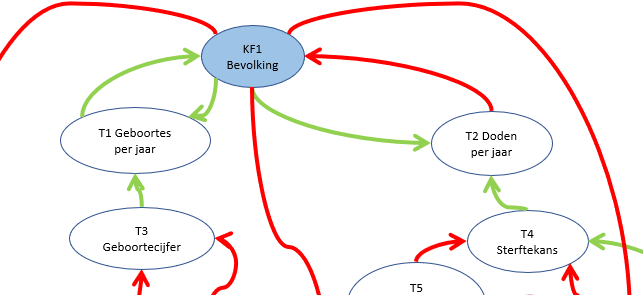
De Bevolkingsgrootte KF1 in jaar t is de grootte in jaar t-1 plus de Geboortes T1 in jaar t minus de Sterftes T2 in jaar t. In het model gaat er een groene pijl van T1 naar KF1, een rode van T2 naar KF1.
Een ander absoluut verband zien we bij KF4: KF4t=T8t/KF1t-1.
Het Voedsel per hoofd KF4 in jaar t is gelijk aan de Hoeveelheid voedsel T8 in jaar t gedeeld door de Bevolkingsgrootte KF1 in jaar t-1. Hoe groter T8 hoe groter KF4 (dus een groene pijl in het model), hoe groter KF1 hoe kleiner KF4 (een rode pijl).
NB we kiezen er voor om te delen door de bevolkingsgrootte in het jaar t-1, omdat we anders het risico lopen op een kringverwijzing: KF4 heeft invloed op de sterftekans T4 en die bepaalt weer de bevolkingsgrootte.
2. Relatief verband
Maar de meeste pijlen in het model vertegenwoordigen een ingewikkelder verband tussen de variabelen. We kunnen bijvoorbeeld niet zeggen dat we de hoeveelheid gezondheidszorg ergens van af trekken om tot een sterftekans te komen.
Maar het is wel aannemelijk dat als de gezondheidszorg van jaar op jaar toeneemt dat dan de sterftekans afneemt (los van andere variabelen). In formulevorm: 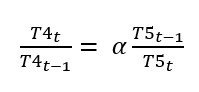 ofwel
ofwel ![]()
NB1 Hoe sterk de invloed van de gezondheidszorg op de sterftekans is, wordt door α bepaald.
NB2 hadden we te maken met een positieve invloed (een groene pijl) dan hadden we de teller en noemer bij T5 omgewisseld.
LET OP We zullen hierna zien dat deze vorm meestal nog te eenvoudig is om het verband tussen variabelen goed te modelleren.
Zoals het er nu uitziet kunnen we het model op basis van deze 2 soorten verbanden gaan beschrijven. In een volgend artikel zal kolom F in het tabblad Beschr van het Voorbeeldbestand gevuld worden met alle gebruikte rekenregels.
Exponentiële groei
Eén van de belangrijkste oorzaken voor de schokkende resultaten van de MIT-studie is gelegen in het feit dat in onze wereld (in ieder geval in het gehanteerde wereld-model) diverse variabelen de neiging hebben tot een exponentiële groei. De belangrijkste daarvan is de bevolking. Hoe dat komt zullen we hierna bekijken.
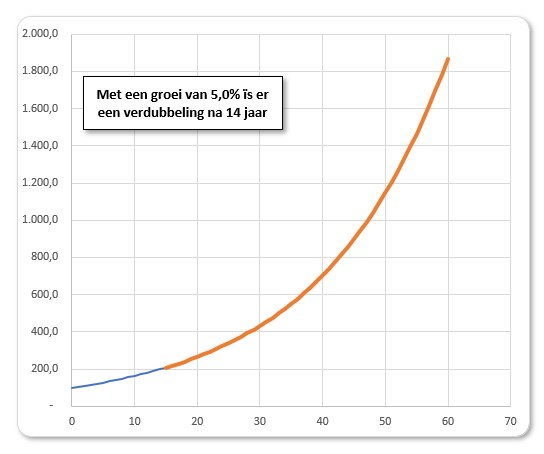
Stel we beginnen met € 100; wanneer we jaarlijks 5% rente krijgen (dat was ooit!) dan hoeven we niet 20 jaar te wachten tot het bedrag verdubbeld is, maar slechts 14 jaar. Dit door het effect van rente op rente. Wacht je dan nog eens 14 jaar dan heb je al 4 keer zoveel.
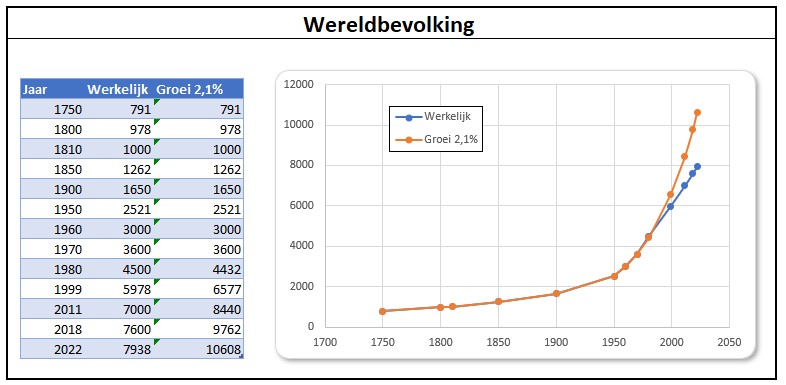
Op het tabblad ExpGroei van het Voorbeeldbestand kun je met het percentage ‘spelen’ om te zien wat het effect daarvan is. De bijbehorende grafiek past zich automatisch aan.
In 1970 was de groeivoet van de wereldbevolking 2,1%. Dit zou een verdubbeling betekenen na 33 jaar. In de grafiek op het tabblad ExpGroei staan de werkelijke groei en de groei met 2,1% vanaf 1970 naast elkaar. Daar valt uit af te leiden dat de groeivoet is gedaald in de loop van de tijd. De consequentie daarvan is dat de verdubbeling niet heeft plaats gevonden in 2003 maar ‘pas’ in 2013.
Bebouwbare grond
Eén van de vele consequenties van de exponentiële groei van de bevolking zien we terug bij de verwachting van de beschikbaarheid van voldoende landbouwgrond.
Volgens de Club van Rome was er in 1970 3,2 miljard ha grond beschikbaar voor landbouw. De verwachting was ook dat dat in de toekomst niet significant zou toenemen; dat zou economisch niet rendabel zijn.
Op dat moment was er wereldwijd per persoon 0,4 ha nodig om voldoende voedsel te kunnen verbouwen (ter illustratie: in de US werd er toen 0,9 ha pp gebruikt).
In het rapport is er ook rekening mee gehouden dat er per persoon 0,08 ha van de beschikbare bouwgrond nodig was voor bewoning en andere infrastructuur.
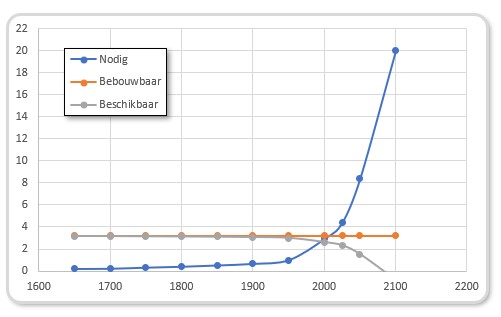
In het tabblad Bebouwbaar van het Voorbeeldbestand is in de grafiek te zien dat er lang (ruim) voldoende grond was om voedsel te verbouwen. Maar door de exponentiële groei van de bevolking stijgt de benodigde hoeveelheid grond na 1970 snel, terwijl de beschikbare hoeveelheid vanaf dat moment versneld gaat afnemen. De 2 lijnen snijden elkaar ongeveer in het jaar 2000.
Gelukkig is die ‘voorspelling’ niet bewaarheid. Waarschijnlijk door een efficiënter gebruik van de grond en de lagere groei van de bevolking.
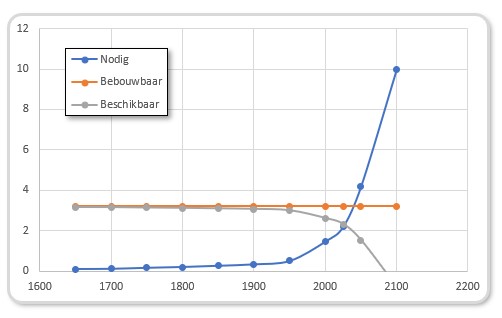
In het tabblad Bebouwbaar kun je de productiviteit aanpassen. Hiernaast staat de grafiek bij een productiviteitsfactor van 2; ofwel er is maar 0,2 ha pp nodig. De 2 lijnen snijden elkaar nu pas in het jaar 2025.
Het mag duidelijk zijn dat een verdere verhoging van de productiviteit en/of verlaging van de groeivoet van de bevolking slechts uitstel betekent tot er niet voldoende landbouwgrond meer is. Gemiddeld over de wereld gaat het nu nog goed, maar mensen in Afrika kijken daar waarschijnlijk al anders tegen aan. Ook de oorlog in Oekraïne laat ons zien, dat een (relatief kleine) verstoring van de normale wereldorde een groot effect op onze voedselvoorziening tot gevolg heeft.
Bevolkingsgroei
In het model, dat we hier hanteren, wordt de grootte van de bevolking alleen bepaald door het aantal geboortes (T1) en doden (T2) per jaar. Zoals hiernaast te zien is bepaalt de grootte van de bevolking (KF1) echter ook weer de aantallen van T1 en T2. Dergelijke terugkoppelingen zien we meer terug in het model en deze zorgen vaak voor het exponentiele karakter van groei.
In het tabblad TerugKoppeling van het Voorbeeldbestand is dit te zien aan de hand van fictieve cijfers.
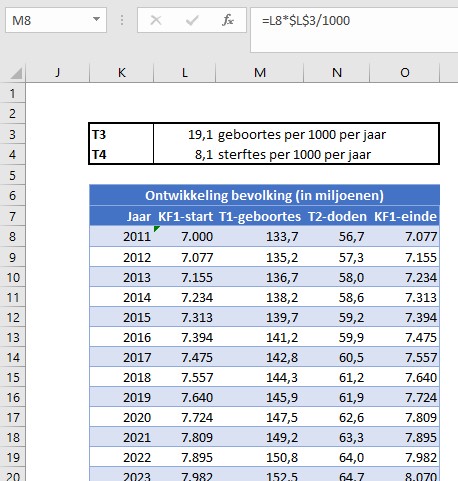
Begin 2011 kende de wereld ongeveer 7 miljard inwoners. Het aantal geboortes per 1000 personen per jaar (Geboortecijfer T3) was toen ongeveer 19,1, terwijl het aantal doden circa 8,1 per 1000 was (Sterftekans T4); de groeivoet van de bevolking per jaar was dus ongeveer 11 per 1000 ofwel 1,1%.
Onder de aanname dat T3 en T4 niet veranderen kunnen we gemakkelijk het verloop van de bevolking over de jaren berekenen.
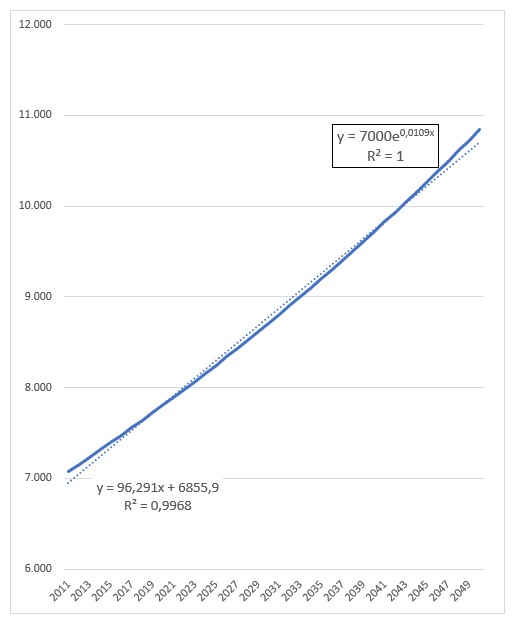
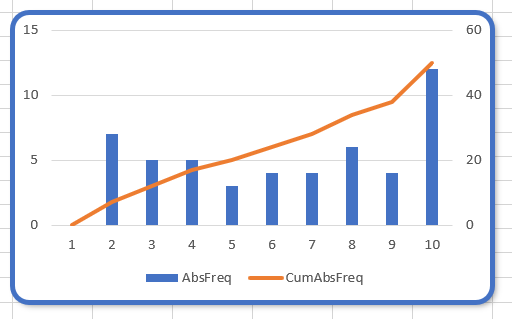
Het verloop is voor 40 jaren berekend en ook in een grafiek uitgezet. We hebben Excel 2 trendlijnen laten bepalen: een lineaire en een exponentiële.
De lineaire voldoet met een R2 van 0,9968 (zie het artikel Trend-analyse) prima op het getekende stuk, maar wel is te zien dat als we deze trend zouden gebruiken om te voorspellen dat we al snel uit de pas zouden lopen.
De andere trendlijn heeft een R2 van 1 en sluit dus exact aan bij de brongegevens (de trendlijn valt samen met de grafiek zelf).
De bevolkingsgroei is dus exponentieel. Op het tabblad ExpGroei kunnen we zien dat een groeivoet van 1,1% betekent dat de bevolking iedere 60 jaar zal verdubbelen.
Vingeroefening 1
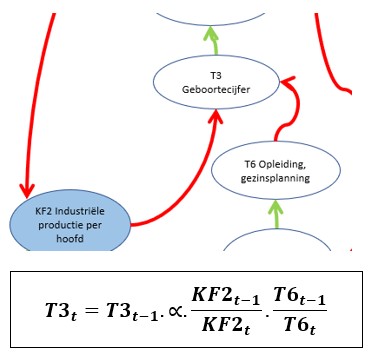
We gaan als eerste eens kijken hoe we de bepaling van het Geboortecijfer T3 kunnen modelleren (zie het tabblad GebCijfer in het Voorbeeldbestand).
Zoals te zien is in het schema wordt T3 beïnvloed door de variabelen KF2 (Industriële productie per hoofd) en T6 (opleiding, gezinsplanning). Bij allebei staat een rode pijl. Dat betekent dat een grotere waarde voor KF2 en/of T6 er voor zorgt dat T3 kleiner wordt (in het Club-rapport wordt de achtergrond hiervan kort uitgelegd).
We hebben hier te maken met een relatief verband; hierboven staat de daarbij behorende formule. Maar daar zitten wel wat haken en ogen aan:
- de formule bevat één α, waarmee we de gevoeligheid van T3 voor veranderingen in KF2 en T6 kunnen regelen. Maar de gevoeligheid per variabele kan verschillend zijn; dat zouden we zichtbaar willen hebben.
- als het gemiddeld opleidingsniveau dit jaar is gestegen ten opzichte van vorig jaar, zal dat niet direct al dit jaar een verandering in T3 geven; daar zit natuurlijk een vertraging in.
- een eenmalige grote wijziging in bijvoorbeeld KF2 hoeft niet ook een dergelijk effect te hebben op T3. Het is beter als we een langere periode dan 1 jaar hanteren om de gemiddelde relatieve wijziging te bepalen.
Wanneer we met deze 3 punten rekening houden wordt de formule ‘iets’ ingewikkelder:
- iedere variabele heeft zijn eigen gevoeligheidsfactor GF. Omdat er in het model straks veel van dit soort factoren zijn, geven we iedere factor een aanduiding mee op welk verband deze betrekking heeft. Bijvoorbeeld GFKF2,T3 is de gevoeligheid van het verband tussen KF2 en T3.
Om decimalen bij de invoer te vermijden schalen we de GF’s tussen 0 en 100.
NB als het resultaat van een verband heel sterk wordt beïnvloed door de bron-variabele kan de GF ook groter dan 100 zijn. - de vertraging in het effect wordt door de V-variabelen in de formule bepaald
- en de periode door de P’s.
NB we bepalen op bovenstaande manier de gemiddelde wijziging tussen het begin en einde van de periode. Voorlopig lijkt dit een goede oplossing, maar misschien blijkt het straks nodig om een gemiddelde over alle wijzigingen in de periode te nemen. Of als het verloop in de periode sterk exponentieel is een nog wat ingewikkelder methode.
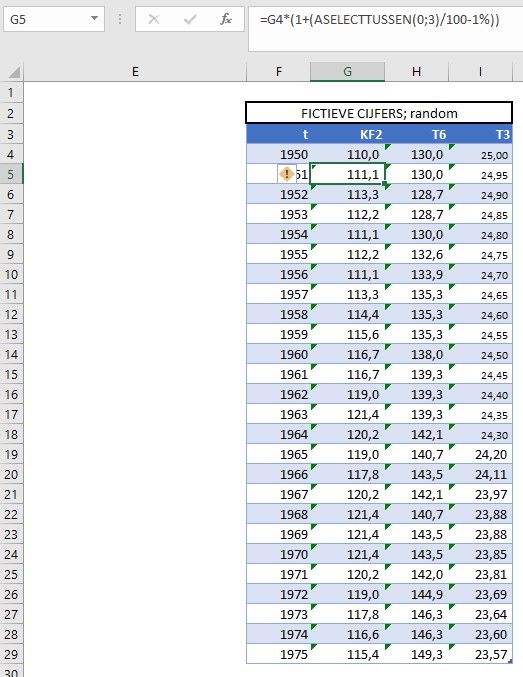
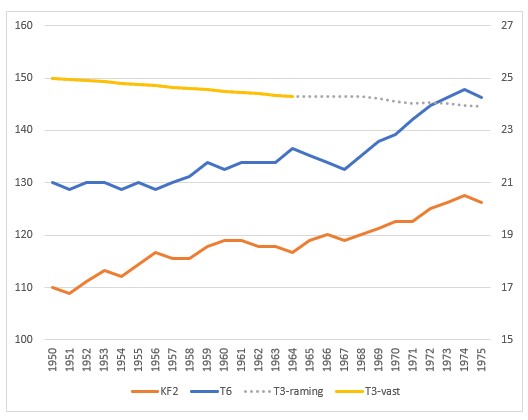
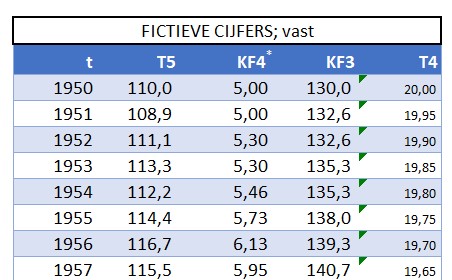
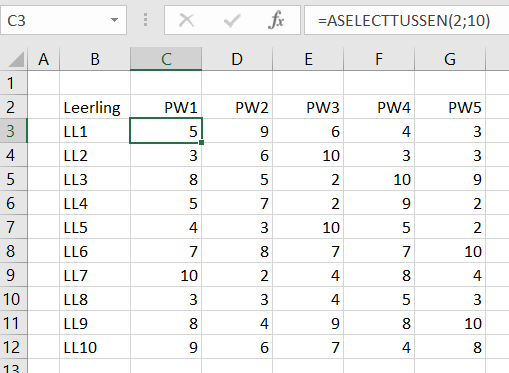
Om wat te kunnen experimenteren staat op het tabblad GebCijfer een tabel met fictieve cijfers over de jaren 1950-1975.
De cijfers over 1950 zijn ‘hard’. Met de formule
=G4*(1+(ASELECTTUSSEN(0;3)/100-1%)) in cel G5 zorgen we dat KF21951 met een waarde tussen -1% en +2% wijzigt ten opzichte van 1950. Op dezelfde manier worden alle cellen in de kolommen G en H met willekeurige waarden gevuld.
De waardes voor T3 zijn voor de jaren tot en met 1964 ‘hard’ ingevuld.
De niet-harde cellen worden telkens opnieuw berekend wanneer op F9 wordt gedrukt.
In cel I19 staat het eerste resultaat van de berekening volgens bovenstaande systematiek:
=I18*
(1+($C$41/100)*
(VERSCHUIVING([@KF2];-$C$39-$C$40;0)/VERSCHUIVING([@KF2];-$C$39;0)-1)/$C$40)*
(1+($C$44/100)*(VERSCHUIVING([@T6];-$C$42-$C$43;0)/VERSCHUIVING([@T6];-$C$42;0)-1)/$C$43)
- de inhoud van cel I18 is de T3 van het vorige jaar
- C41 is de waarde van GFKF2,T3
- C39 is de VKF2,T3
- en C40 is de PKF2,T3
De functie Verschuiving selecteert op basis van (in dit geval) 3 parameters een cel:
- de eerste parameter is de start-positie van de selectie; hier de cel in de kolom met de naam T6, die in dezelfde regel staat als de formule ([T6] is de hele tabel-kolom, [@T6] alleen de cel in dezelfde regel).
- de tweede is het aantal rijen naar beneden of naar boven voor de daadwerkelijke selectie
- en de derde geeft aan of de selectie naar links of rechts ten opzichte van de start-positie moet plaats vinden
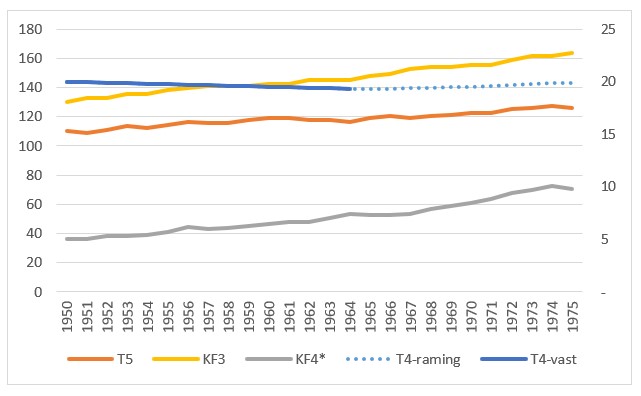
Op het tabblad GebCijfer staat naast de tabel met random-waarden ook een tabel waarin alle waarden in de kolommen KF2 en T6 vast zijn. Op deze manier kun je beter zien wat de consequenties van aanpassingen van de GF-, V– en P-parameters zijn voor het resultaat. De grafieken laten het effect goed zien.
Het beoordelen van het resultaat voor wijzigingen in alleen KF2 of T6 kan eenvoudig door de andere GF op 0 in te stellen.
Vingeroefening 2
Het tabblad SterfteKans van het Voorbeeldbestand bevat een ander gedeelte van het vereenvoudigde model.
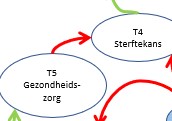
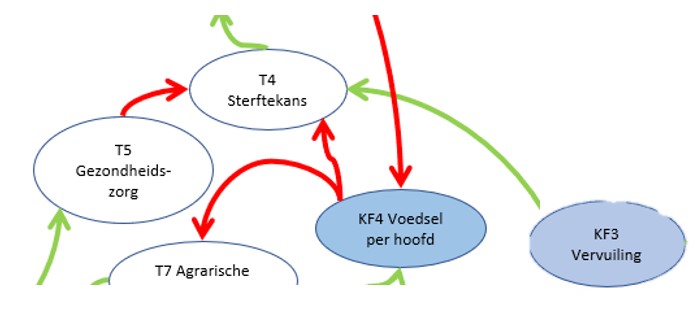
We zien hier dat de Sterftekans T4 door 3 variabelen wordt beïnvloed: T5 Gezondheidszorg, KF4 Voedsel per hoofd en KF3 Vervuiling.
We zien 2 rode en 1 groene pijl: als T5 en/of KF4 stijgen zal de sterftekans dalen, maar wanneer de vervuiling toeneemt, neemt ook de T4 toe.
De verbanden tussen de variabelen T5-T4 en KF3-T4 kunnen we modelleren als in de vorige vingeroefening. De relatie tussen KF4 en T4 is ingewikkelder. Wanneer de hoeveelheid voedsel per hoofd blijft stijgen zal dat geen verdere daling van de sterftekans met zich meebrengen (misschien zelfs integendeel).
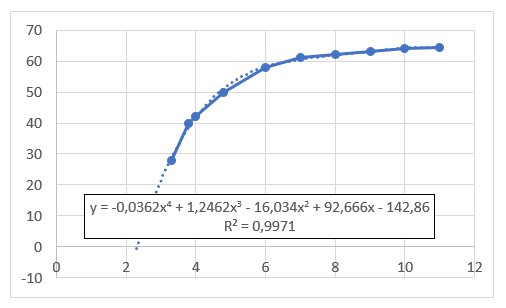
In het Club-rapport is wel een verband gevonden tussen het voedingsniveau (uitgedrukt in groente calorie-equivalenten) en de gemiddelde verwachte levensduur (situatie 1953). Een trendanalyse laat zien, dat dit verband zich goed laat benaderen door een 4e graadsfunctie (tenminste op het relevante stuk met een voedingsniveau tussen 3 en 12). Deze functie zullen we hierna SK_4 noemen.

De formule (zie het tabblad StefteKans) wordt er niet simpeler op!
In het tweede blok gebruiken we dus niet de verhouding tussen twee waardes van KF4, maar de verhouding tussen twee uitkomsten van SK_4(KF4*).
NB we moeten straks bij de implementatie van het model de waardes van KF4 schalen naar een waarde tussen 3 en 12.
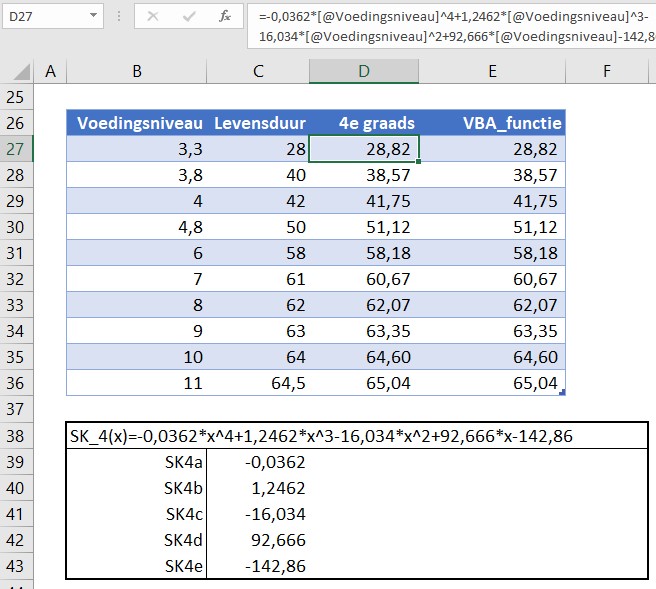
In een tabel op het tabblad SterfteKans hebben we de gegevens uit het Club-rapport overgenomen. In kolom D staat de berekening volgens de 4e graadsfunctie; de verschillen zijn marginaal.
Onder de tabel zijn de 5 benodigde parameters voor de functie opgenomen; de cellen hebben overeenstemmende namen gekregen.
Deze namen gebruiken we in de eigen functie SK_4; deze functie zullen we straks in de modelberekeningen gebruiken in plaats van formules met cel-verwijzingen.
NB1 voor uitleg over eigen functies, zie het betreffende artikel.
NB2 de functie bevat ook een underscore, omdat Excel anders denkt dat het een verwijzing is naar de cel in kolom SK en rij 4.
Ook nu hebben we een overzicht gemaakt met fictieve gegevens. Door met de diverse parameters te spelen krijg je gevoel voor de samenhang tussen de diverse variabelen. De bijbehorende grafiek ondersteunt daarbij.
Het volgende artikel van G-Info zal gewijd zijn aan de implementatie van het vereenvoudigde model. Daar liggen wel wat uitdagingen; technisch maar zeker ook bij het vullen van de diverse parameters. Er zullen heel wat aannames gedaan moeten worden. En of de resultaten van het model dan lijken op de uitkomsten van de Club van Rome? We zullen het zien.








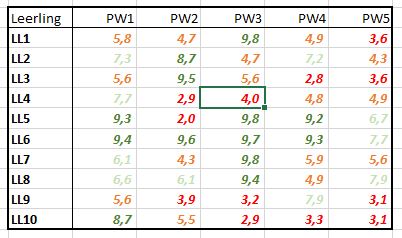
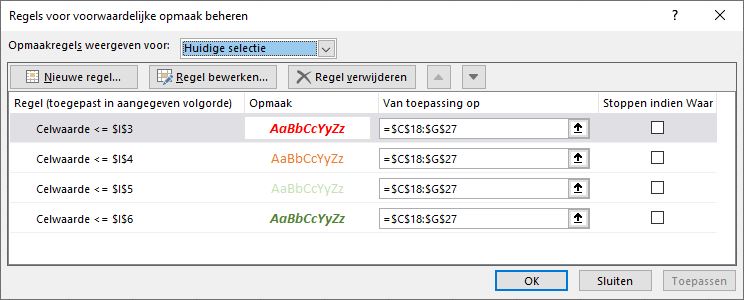
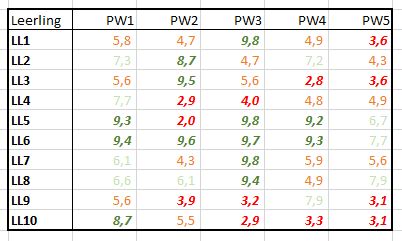
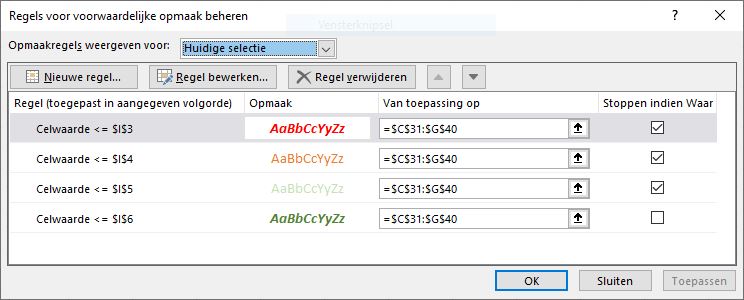

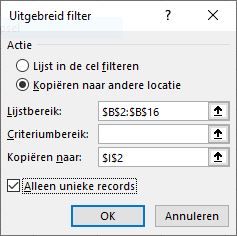
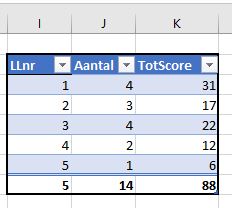
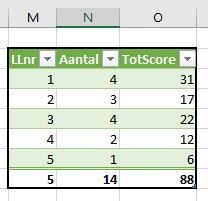
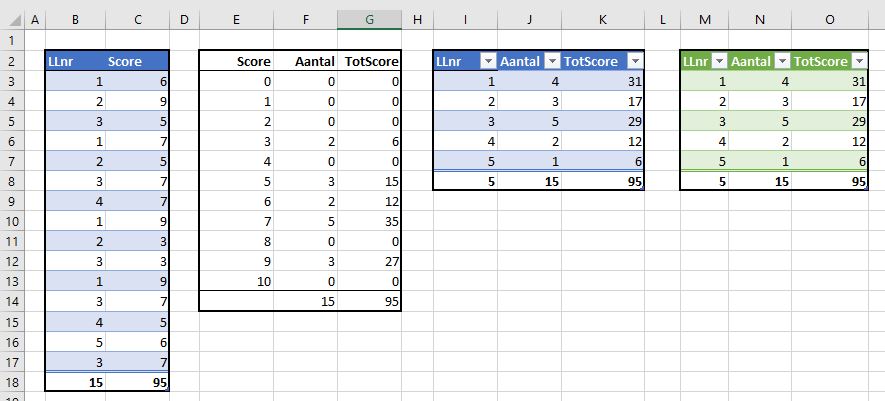


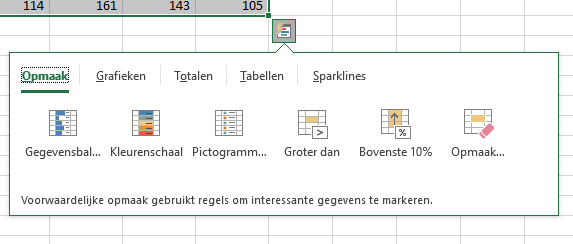
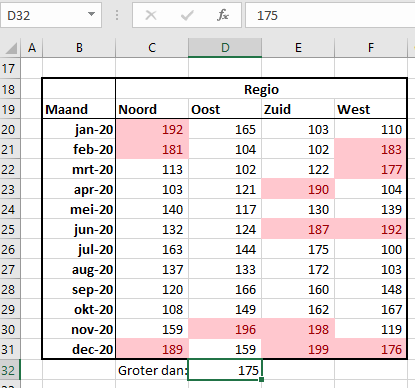
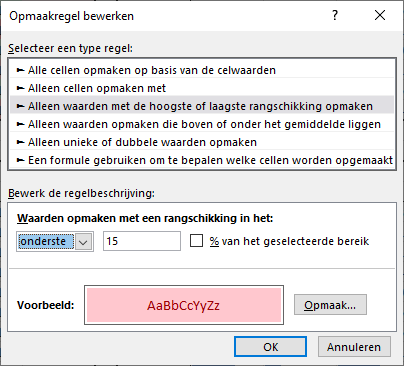
 kun je bestaande opmaak wissen.
kun je bestaande opmaak wissen.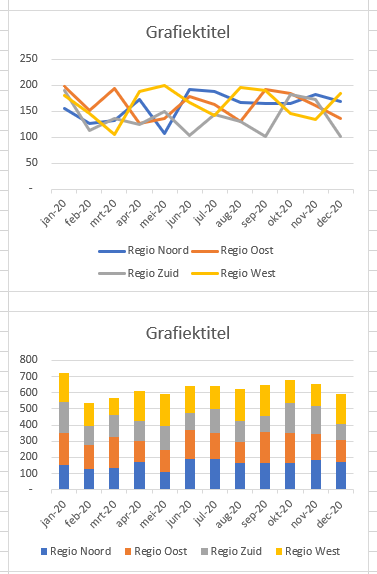

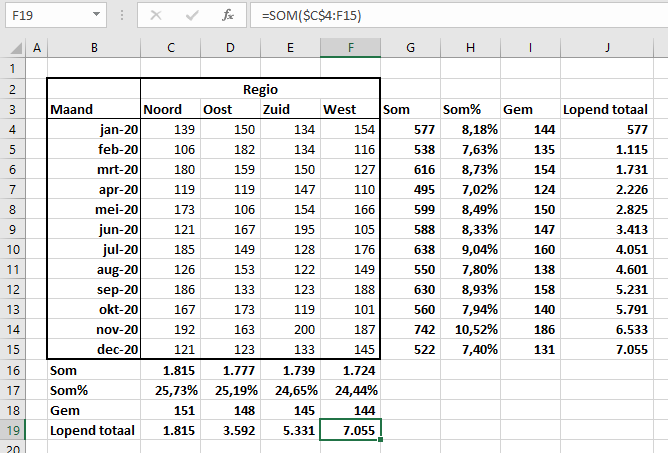
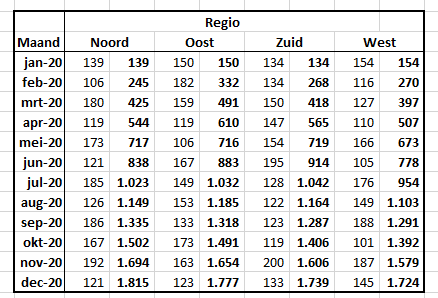
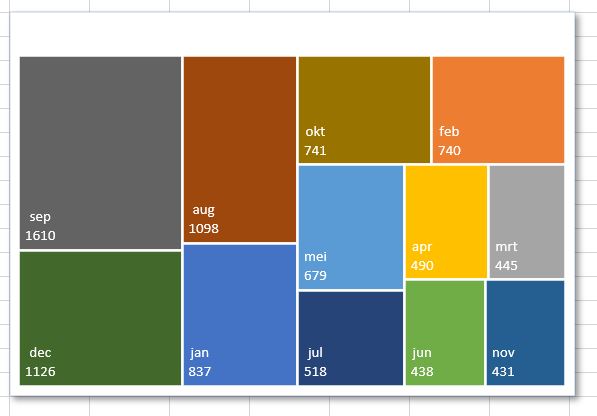
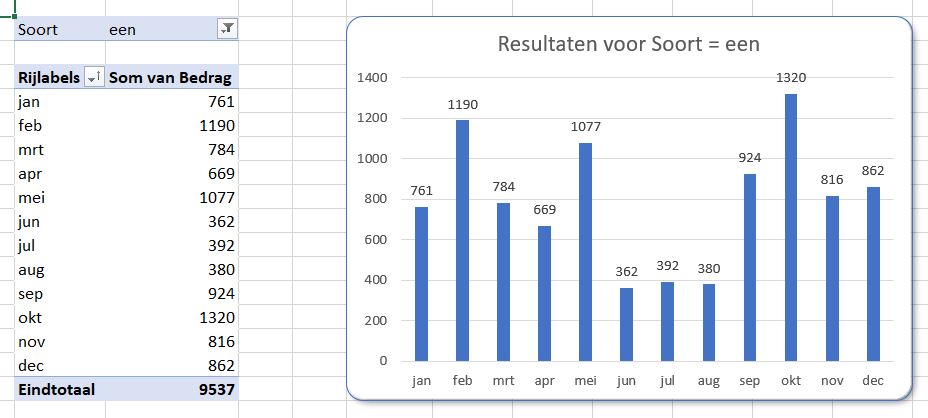
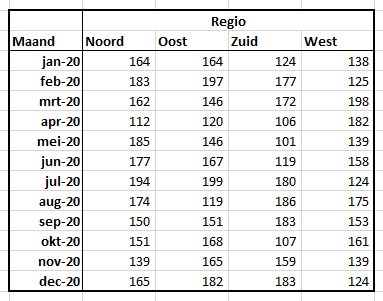
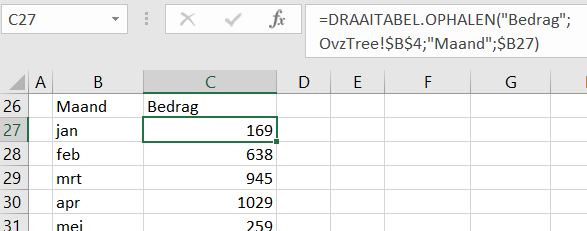
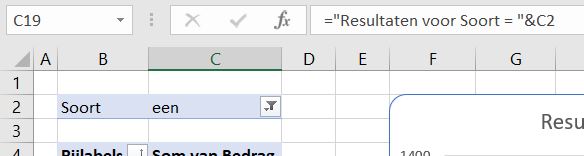 In cel C19 wordt de basis daarvoor gelegd. U wijzigt een grafiektitel als volgt: klik in de bestaande titel, daarna in de formulebalk, voer het =-teken in, klik dan op cel C19 en druk op Enter. In de formulebalk verschijnt =OvzTree!$C$19.
In cel C19 wordt de basis daarvoor gelegd. U wijzigt een grafiektitel als volgt: klik in de bestaande titel, daarna in de formulebalk, voer het =-teken in, klik dan op cel C19 en druk op Enter. In de formulebalk verschijnt =OvzTree!$C$19.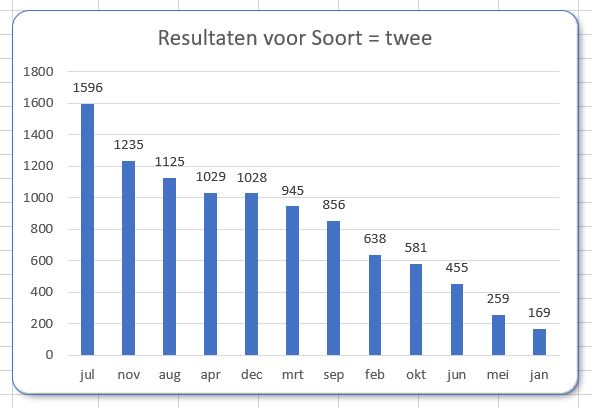
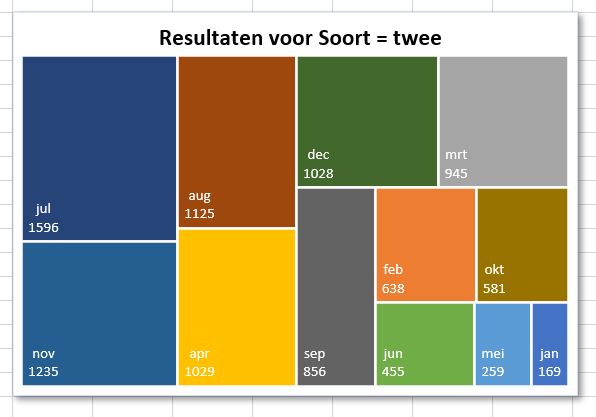
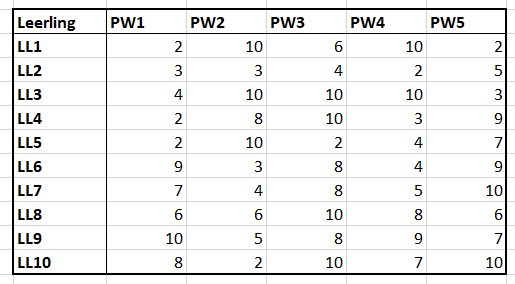
 Vorige week kreeg ik de vraag, hoe je met Excel het makkelijkst de winnaars van een wedstrijd zou kunnen selecteren.
Vorige week kreeg ik de vraag, hoe je met Excel het makkelijkst de winnaars van een wedstrijd zou kunnen selecteren.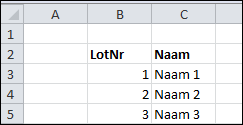 In het
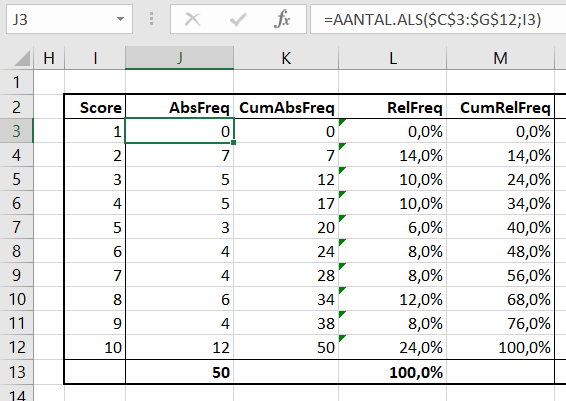
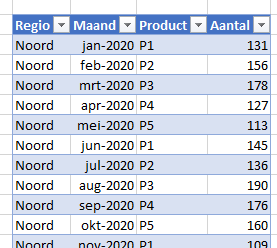
In het 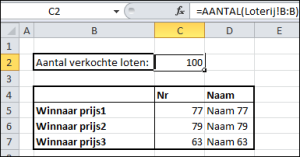 Op het tabblad Uitslag worden 3 winnaars geselecteerd:
Op het tabblad Uitslag worden 3 winnaars geselecteerd: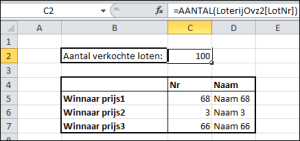 De formule in C2 ziet er anders uit:
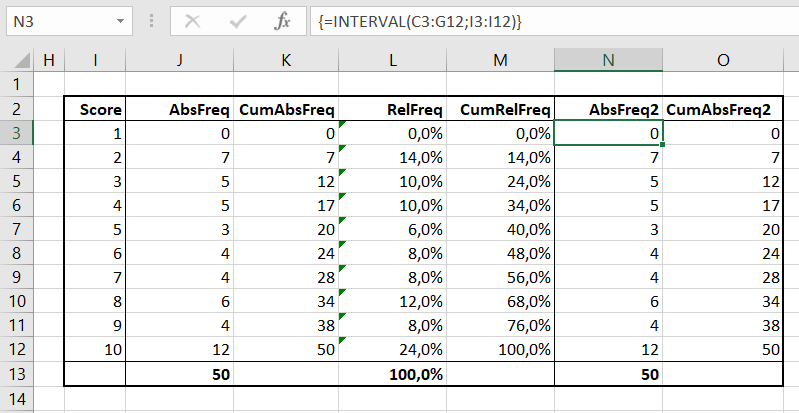
De formule in C2 ziet er anders uit: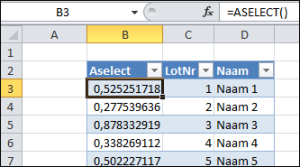 In het tabblad Loterij3 van het
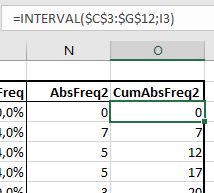
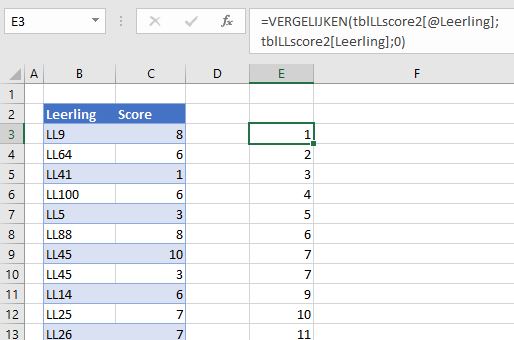
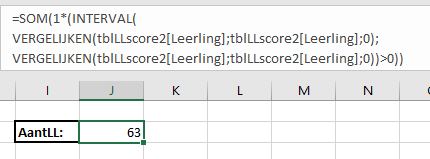
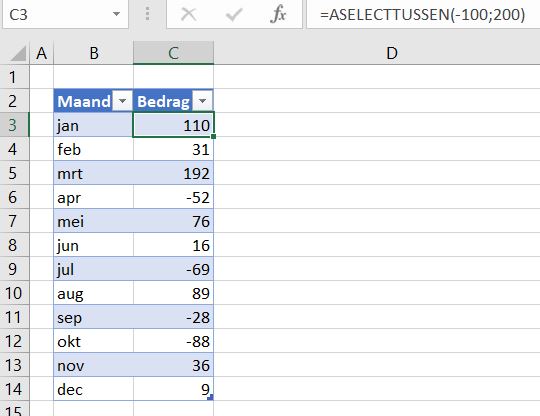
In het tabblad Loterij3 van het 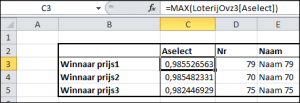 De bepaling van de winnaars gaat nu iets anders: in cel C3 wordt de eerste winnaar bepaald door het grootste getal (MAX) in de kolom Aselect van de tabel LoterijOvz3 op te zoeken. In D3 wordt met VERT.ZOEKEN het corresponderende lotnummer gevonden en in E3 met INDEX de naam (zoals uit de formules van kolom F blijkt kunnen we dat laatste ook met VERT.ZOEKEN in de hele tabel LoterijOvz3).
De bepaling van de winnaars gaat nu iets anders: in cel C3 wordt de eerste winnaar bepaald door het grootste getal (MAX) in de kolom Aselect van de tabel LoterijOvz3 op te zoeken. In D3 wordt met VERT.ZOEKEN het corresponderende lotnummer gevonden en in E3 met INDEX de naam (zoals uit de formules van kolom F blijkt kunnen we dat laatste ook met VERT.ZOEKEN in de hele tabel LoterijOvz3).