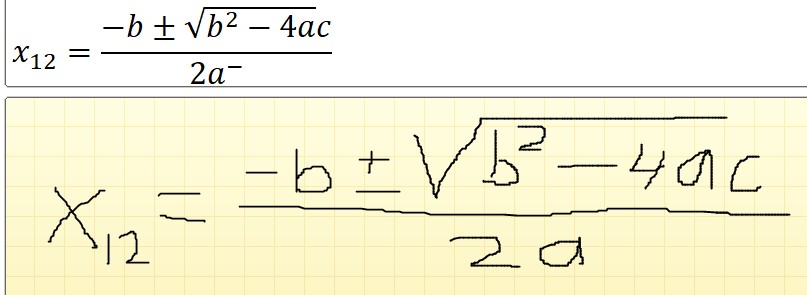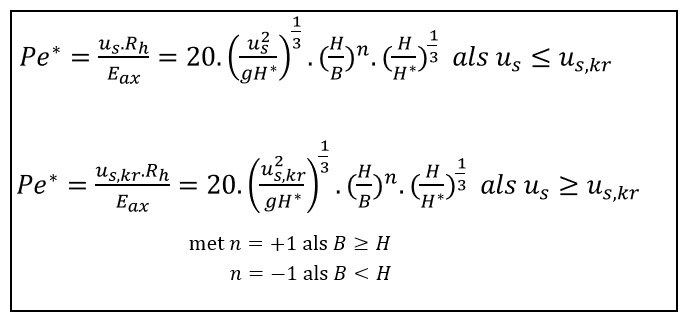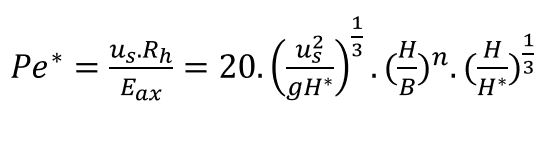
Binnen Excel, maar beter gezegd binnen alle Office-onderdelen, is het mogelijk om allerlei nuttige, mooie en/of grappige Symbolen in te voegen.
Maar niet alleen symbolen, ook (wat Microsoft noemt) Vergelijkingen. Daarmee wordt het opzetten van een documentatie-tabblad in Excel of een technisch artikel in Word a-piece-of-cake 😉.
In dit artikel zoomen we in op de diverse mogelijkheden om symbolen in te voegen en op het maken van Vergelijkingen. We maken daarbij gebruik van Excel, maar in de andere Office-onderdelen is de werkwijze vergelijkbaar.
Ook zullen we aandacht besteden aan de zogenaamde ASCII– en Unicodering.
Symbolen-1
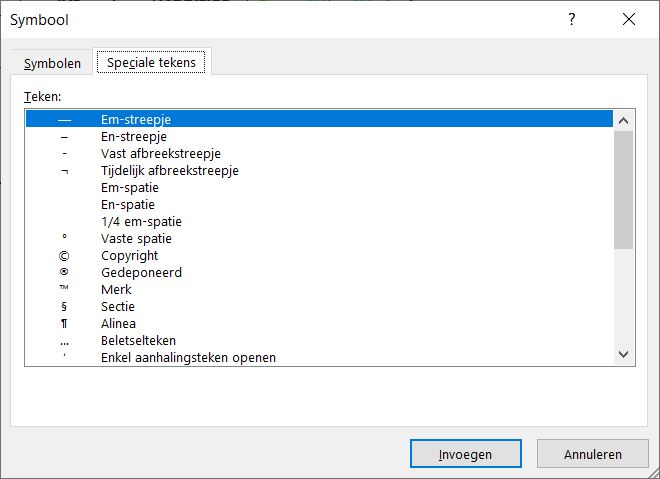
Er zijn allerlei manieren om symbolen in te voeren. De eerste die we hier behandelen is het invoegen van Speciale tekens. Kies in de menutab Invoegen in het blok Symbolen de optie Symbool: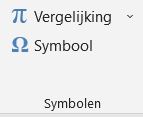
In de pop-up selecteert u het tabblad Speciale tekens. Kies bijvoorbeeld het copyright-teken en klik op Invoegen (of dubbelklik op het teken).
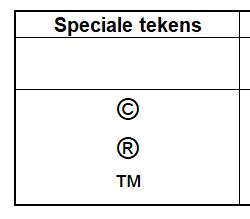
Op het tabblad Symbolen van het Voorbeeldbestand ziet u het resultaat.
LET OP wat er op het scherm wordt weergegeven is afhankelijk van het gekozen lettertype voor de cel. Wijzig het lettertype voor de range B4:B6 in Wingdings en het resultaat is ![]()
Symbolen-2
Wanneer bovengenoemde pop-up tevoorschijn komt, is altijd automatisch het tabblad Symbolen geactiveerd.
NB1 maak het pop-up-scherm groter om een beter overzicht van alle mogelijkheden te krijgen.
Selecteer het gewenste symbool en klik op Invoegen.
NB2 De meeste lettertypes bevatten veel meer symbolen dan je zou denken. Zorg ervoor dat onderaan bij van: de optie Unicode (hex) is gekozen; je kunt dan diverse deelverzamelingen kiezen: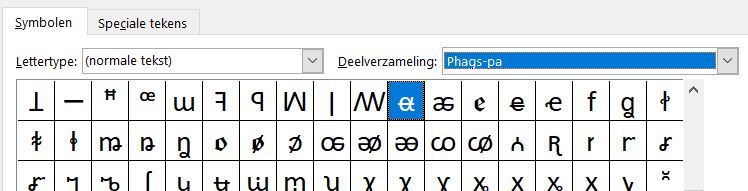
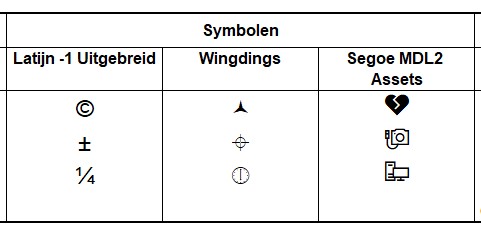
In het tabblad Symbolen van het Voorbeeldbestand zijn op bovenstaande manier symbolen ingevoegd. De symbolen in de eerste kolom komen uit de deelverzameling Latijn-1; als achteraf het lettertype van deze kolom gewijzigd wordt, dan zullen de symbolen er vaak nog hetzelfde uitzien met slechts typografische verschillen.
Maar kies je bijvoorbeeld als lettertype Wingdings dan is de inhoud ineens anders (zie 2e kolom)! Dit is dan ook een lettertype vol met vreemde symbolen. Er is standaard ook nog een tweede en derde versie van dit font. Het lettertype Segoe MDL2 Assets zit vol met verrassingen (zie kolom 3). Ook met het lettertype Webdings kun je veel mooie symbolen tevoorschijn toveren.
LET OP niet iedere Windows-versie kent dit tweede font; soms kom je Segoe-symbol tegen.
ASCII versus Unicode
Voordat we verder gaan over symbolen moeten we aandacht besteden aan de coderingen van letters en andere symbolen.
In het begin van het computertijdperk is de ASCII-codering bedacht. Ieder teken werd door 1 byte voorgesteld (eigenlijk pas later in de Extended ASCII) met als consequentie dat er maar 256 mogelijkheden waren. Dat was toen geen probleem: alle hoofd- en kleine letters, cijfers en leestekens passen daar in. Zoals hierboven te zien is was er ook voorzien in de meest gangbare breuken, Griekse letters en letters met diakritische tekens.
Later zijn daar de Unicodes bijgekomen; in versie 2.0 is er plaats voor een miljoen tekens. Ruim voldoende voor diverse talen en andere nuttige symbolen.
Wat kunnen we zelf met die codes? Uiteraard zijn die niet (allemaal) te onthouden. Maar natuurlijk wel van symbolen die we vaak nodig hebben; dan is het lastig als je iedere keer in die hele serie symbolen moet gaan zoeken.
Laten we een voorbeeld nemen; het graden-teken.
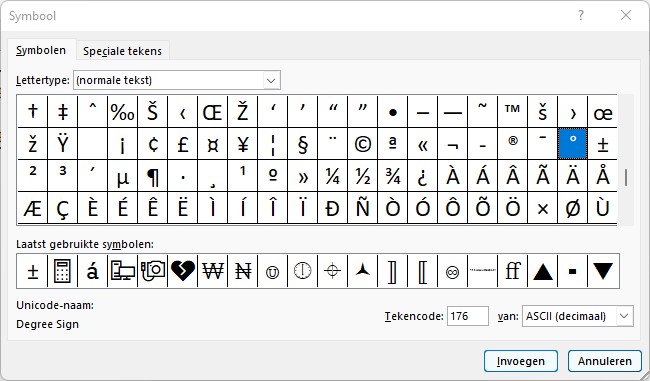
Even zoeken maar dan hebben we hem; onderaan de pop-up is te zien dat dit symbool in ASCII de (decimale) code 176 heeft. Kiezen we voor de optie Unicode (hex) dan is de code 00B0: ![]()
Hebben we nu weer het graden-teken nodig: open het pop-up-scherm, kies een van de 2 coderingen en voer bij Tekencode de overeenkomende code in en klik op Invoegen.
Symbolen-3
Als een lettertype/font symbolen kent die binnen de ASCII-codes voorkomen (en dus een Tekencode hebben in de soort ASCII) dan kunnen deze symbolen nog veel sneller ingevoerd worden (zie het tabblad Symbolen):
- tik in een cel de tekst Het is nu 19 (inclusief de spatie achter de 9)
- hou de Alt-toets ingedrukt en tik op het numerieke toetsenbord de code 0176 in.
- tik in C en druk op Enter.

NB1 deze Alt-invoer kan alleen met de numerieke toetsen aan de rechterkant van het toetsenbord; zorg wel dat de NumLock aanstaat.
NB2 voor een uitgebreidere toelichting over codes zie www.vreemdetekens.nl/
LET OP ASCII-codes vanaf 128 moeten bij dit type invoer voorafgegaan worden door een 0 (nul).
Symbolen-4
Wanneer je de Unicode van een symbool weet kun je deze ook nog op een andere manier gebruiken.
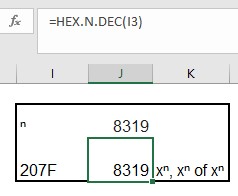
Stel dat we de n (superscript-n) willen gebruiken (zie het tabblad Symbolen van het Voorbeeldbestand).
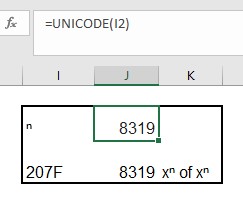
Via bovenstaande methode kunnen we zien dat deze de Unicode 207F heeft (een hexadecimaal getal).
In cel J2 gebruiken we de Excel-formule Unicode om de code van het symbool in I2 op te halen. Het resultaat is nu 8319; dit is de decimale code.
In cel J3 zien we dat dit klopt; hier is de hexadecimale code omgezet naar een decimaal getal met behulp van de Excel-formule Hex.n.dec.
In cel K3 gebruiken we 3 verschillende methoden om xn te schrijven:
=”x”&UNITEKEN(J3)&”, x”&UNITEKEN(HEX.N.DEC(I3))&” of x”&I2
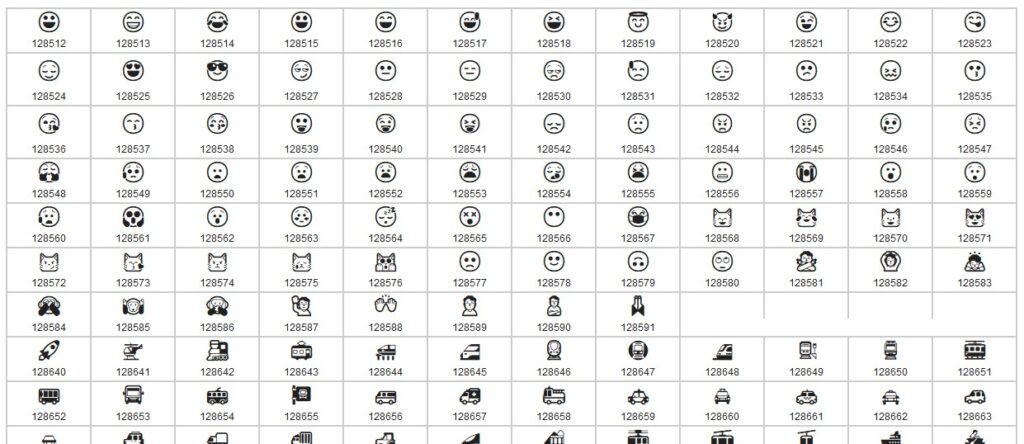
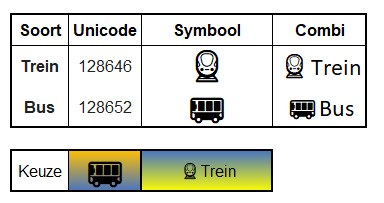
Op het tabblad Unicode van het Voorbeeldbestand ziet u een groot overzicht van allerlei symbolen met de daarbij behorende code.
Ook laten we daar zien hoe je symbolen in een Gegevensvalidatie gebruikt, inclusief het gebruik van de codes in een Voorwaardelijke opmaak.
Symbolen-5
Misschien nog wel de makkelijkste methode om symbolen in te voegen is kopiëren-plakken!
Kijk of je ergens het gewenste symbool kunt vinden (bijvoorbeeld op www.vreemdetekens.nl) , selecteer het met de muis, Ctrl-C, ga naar de gewenste plaats in Excel en Ctrl-V.
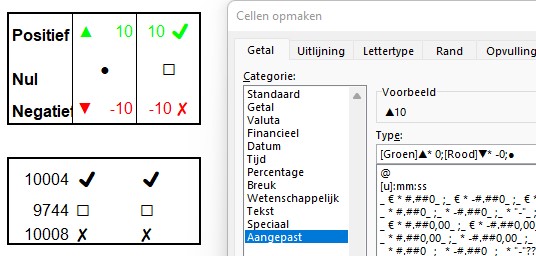
Op het tabblad Symbolen hebben we deze methode gebruikt om een aangepaste getal-opmaak te definiëren in de kolommen N en O.
Symbolen-6
Als laatste een methode die overal in Windows werkt (vanaf Windows-10): druk de Windows-toets (![]() ) in, hou vast en druk dan op de punt-komma-toets.
) in, hou vast en druk dan op de punt-komma-toets.
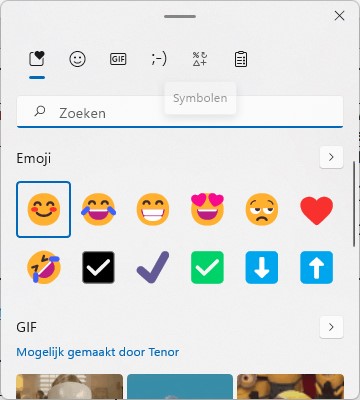
Onderstaande pop-up opent waarna u de beschikking hebt over een arsenaal aan nuttige (?) symbolen.
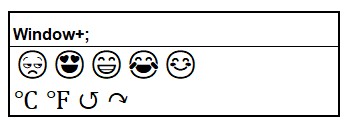
Vergelijkingen (standaard)
Excel kent ook een menu-optie Vergelijking; ook te vinden via de menutab Invoegen in het blok Symbolen. Achter het vinkje zit een serie standaard-formules. Fijn, maar het is wel een paar weken geleden dat ik een Fourier-reeks nodig heb gehad 😁.
Achter het vinkje zit een serie standaard-formules. Fijn, maar het is wel een paar weken geleden dat ik een Fourier-reeks nodig heb gehad 😁.
Laten we maar aannemen dat ze als voorbeeld bedoeld zijn. Klik op één van deze voorbeelden en het resultaat komt in Excel terecht: 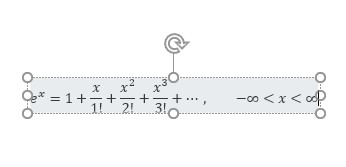
Via de hendels kunt u het formule-blok verschuiven, de grootte wijzigen en via de menutab Hulpmiddelen voor tekenen/Opmaak, die nu beschikbaar is gekomen, kunnen diverse opmaak-opties ingesteld worden. Wilt u de lettergrootte aanpassen? Gebruik de mogelijkheden in de menutab Start.
NB het lettertype wordt automatisch ingesteld op Cambria Math; dit is niet te wijzigen.
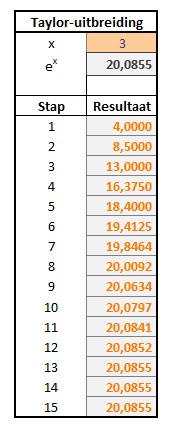
Op het tabblad Verg1 van het Voorbeeldbestand staan enkele standaard-formules. Ook hebben we daar even gecontroleerd of de Taylor-uitbreiding voor het berekenen van ex wel klopt😉
De standaard-formules kunnen wel gebruikt worden als basis om andere formules te ‘schrijven’, want alle formules zijn nog aanpasbaar.
Vergelijkingen (handmatig)
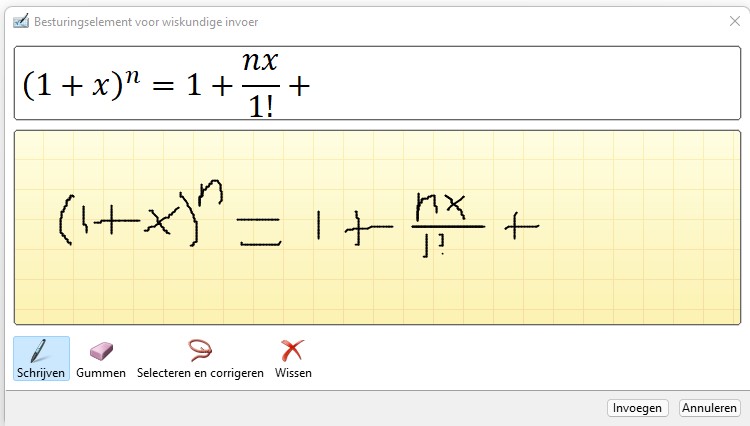
Over schrijven gesproken: je kunt de gewenste formule/vergelijking handmatig invoeren: kies in de menutab Invoegen in het blok Symbolen het vinkje achter Vergelijking. Helemaal onderaan staat dan de optie Handgeschreven vergelijking.
Met wat proberen, Gummen, Selecteren en corrigeren en opnieuw Schrijven kom je al snel een heel eind.
Maar het lukte mij niet om de komma tussen de 1 en de 2 te krijgen; ook het extra streepje achter de a in de noemer kreeg ik niet weg.
Gelukkig: na het kiezen van Invoegen in de pop-up kan de door Excel gegenereerde formule nog gewijzigd worden: 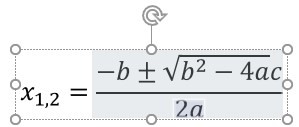
Vergelijking (kwadratische formule)
In de standaard-vergelijkingen van Excel komen ook de stelling van Pythagoras en de kwadratische formule voor (zie het tabblad Verg2 van het Voorbeeldbestand). De laatste wordt in het wiskundeonderwijs meestal de abc-formule genoemd.
In de standaardformule (rood omcirkeld) staat voor het =-teken alleen x. Meestal gebruiken we x1,2 om aan te geven dat er in principe 2 oplossingen zijn van een 2e graadsvergelijking; de eerste krijgen we door de + voor het wortelteken, de tweede door de wortel af te trekken van -b.
De ‘groene’ formule is veel beter leesbaar dan ![]()
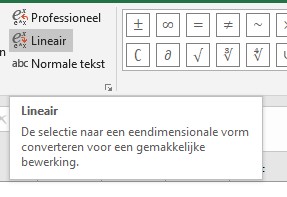
Dit is de zogenaamde Lineaire vorm (in tegenstelling tot de vorige die Professioneel wordt genoemd). Je kunt als volgt switchen tussen de twee verschijningsvormen
- selecteer een formule door er op te klikken
- er verschijnt een nieuwe menutab Hulpmiddelen voor vergelijkingen
- klik daar op het tabblad Ontwerpen
- in het blok Extra vooraan ziet u de 2 opties
Het voordeel van de Lineaire variant is, dat deze soms makkelijker te corrigeren is.
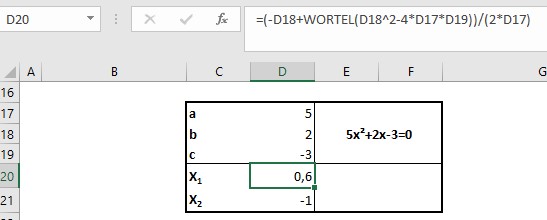
In het tabblad Verg2 gebruiken we de abc-formule om de oplossingen van 2e graadsvergelijkingen te vinden.
Wanneer we de cellen D17:D19 namen geven is de formule veel beter leesbaar:
=(-b+WORTEL(b^2-4ac_))/(2*a)
NB voor cel D19 kunnen we niet de naam c gebruiken (een gereserveerde code voor Excel), vandaar de underscore erachter.
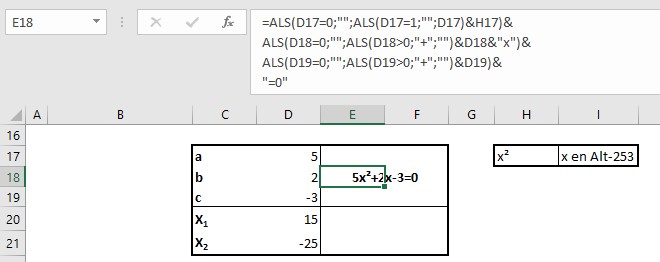
In de formule in E18 wordt gebruik gemaakt van de inhoud van cel H17. Deze bevat een x met het symbool 2 (Alt-253).
NB de overgangen naar een nieuwe regel in de formule zijn voor de leesbaarheid; druk op Alt-Enter.
Vergelijking (hypotheek)
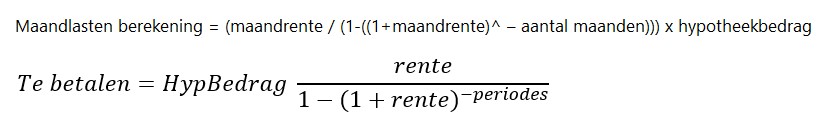
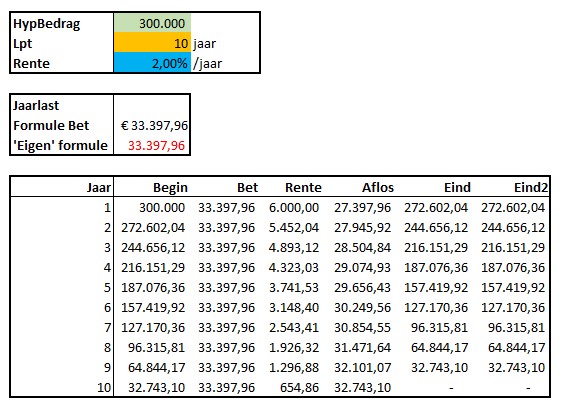
In het tabblad Hyp staat een voorbeeld van een hypotheekberekening.
Excel kent daarvoor de standaard-functie Bet, maar zoals je hierboven kunt zien kun je ook een ‘eigen’ formule gebruiken.
Door gedeeltes van de toelichtende vergelijking dezelfde kleuren te geven als de overeenkomende cellen wordt snel het verband duidelijk: 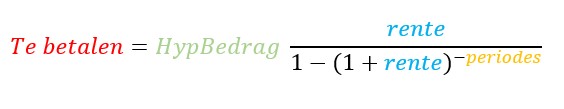
Grenzen aan de groei
Een ander voorbeeld van een formule die je binnen de Office-onderdelen makkelijk kunt maken, komt uit het ‘rapport van de Club van Rome’.
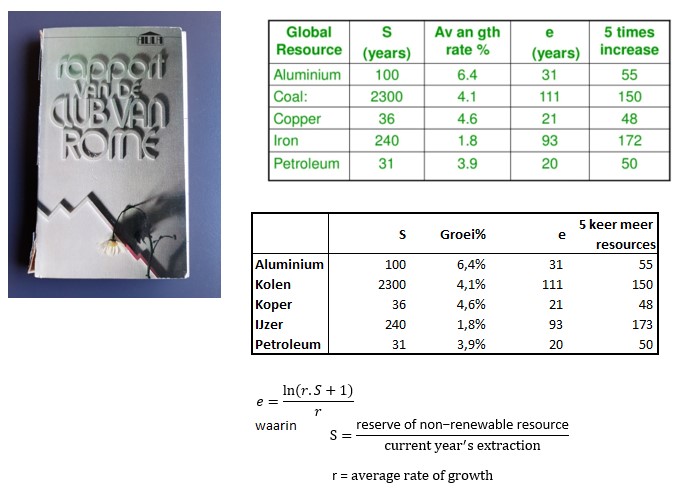
Als je de voorraad van (in dit geval) grondstoffen weet en ook de hoeveelheid die je per jaar nodig hebt, dan weet je ook hoeveel jaar je nog vooruit kunt met die voorraad (de S hierboven). Maar een van de fundamentele bijdrages van de ‘club’ aan de discussie was om ook rekening te houden met de groei van de behoefte. Dit levert het aantal jaren op dat je werkelijk vooruit kunt (e). Deze is vaak dramatisch lager dan de S!
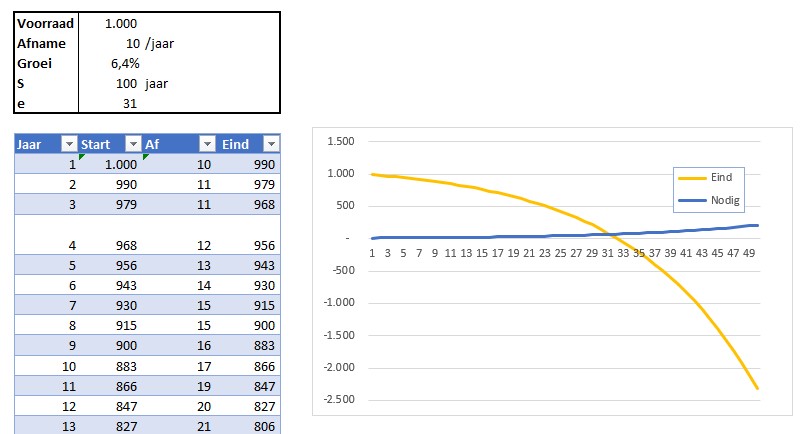
In het tabblad Groei van het Voorbeeldbestand is het effect van de groei van de behoefte grafisch weergegeven.
Binnenkort eens kijken of we de andere variabelen uit het model ook kunnen vinden, inclusief de aannames die daar zijn gebruikt. Dan kunnen we proberen het model in Excel na te bouwen.
Technologie
Nog maar even verder op de nostalgische tour. Tijdens mijn studie op de THE kregen we een handboekje (voor ƒ 1,00). Vol met interessante formules en grafieken.

Laten we de formule voor het Reynolds-getal eens gaan opbouwen (zie het tabblad Technologie van het Voorbeeldbestand):
- kies in de menutab Invoegen in het blok Symbolen de optie Vergelijking (dus NIET op het vinkje erachter klikken). Een blok met Typ hier uw vergelijking komt tevoorschijn in het midden van het scherm.
- tik in Re=
- nu moet er een breuk komen: klik in de menutab Ontwerpen in het blok Structuren op het vinkje onder Breuk
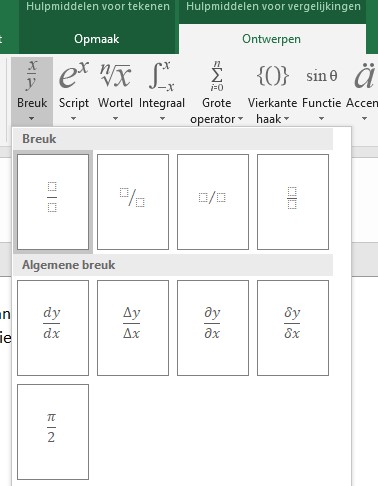
- we kiezen de eerste breuk, waarbij de gestippelde vierkantjes aangeven dat daar nog iets ingevuld kan worden
- selecteer het vierkantje in de teller en klik op het knopje Meer, rechtsonder bij Symbolen. Kies daar de ρ (Griekse letter rho).
- de rest van de teller is dan eenvoudig; tik in .U.2m
- selecteer het vierkantje in de noemer en klik op het knopje Meer, rechtsonder bij Symbolen. We hebben de η (eta) nodig; die is niet te vinden bij Elementaire wiskunde. Kies rechtsboven bij Symbolen de optie Griekse letters en zoek de juiste letter.
- klik ergens buiten het formuleblok.
LET OP als je een formule gaat opbouwen zorg dan dat je elke keer goed vooruitkijkt. Zoals hiervoor bij het maken van een breuk moet je eerst de breuk-optie kiezen waarna je dan pas de teller en noemer kunt invullen.
Wil je x2 tikken, kies dan eerst optie één binnen Script en vul dan de twee vierkantjes met de x en de 2 (of selecteer de 7e optie natuurlijk!).
NB door te switchen naar Lineair (zie hierboven) is het mogelijk om bijvoorbeeld een vergeten breuk te corrigeren door achter de bestaande formule een / te plaatsen. Ga daarna weer naar Professioneel.
Het vergt wat onderzoek om alle mogelijkheden voor het maken van formules te doorgronden. Zelfstudie is zeer noodzakelijk. Zoals eerder gezegd werkt het in de praktijk prima om eerst ‘met de hand’ zo goed mogelijk de formule te schrijven en dan met de Excel-hulpmiddelen zo nodig nog aanpassingen door te voeren.
Afstudeerscriptie
Naar aanleiding van de voorgaande voorbeelden herinnerde ik me dat mijn afstudeerscriptie (van 1978) vol stond met formules, die gedeeltelijk met een typemachine en gedeeltelijk met de hand moesten worden gemaakt (zie hiernaast).
Wanneer er ergens iets fout was (of er moest nog wat tekst tussen) dan moest zo’n pagina opnieuw. Soms kon je gelukkig volstaan met letterlijk knippen en plakken.
NB Wanneer je een keer de slaap niet kunt vatten, kan ik deze lectuur van harte aanbevelen: pure.tue.nl/ws/portalfiles/portal/86904037/297491.pdf
In het tabblad Menging van het Voorbeeldbestand heb ik het belangrijkste resultaat van mijn onderzoek nog eens nagebouwd. Binnen een paar minuten was dat gebeurd, terwijl dat toen op een typemachine heel wat meer tijd kostte.
En een correctie doorvoeren is een fluitje van een cent.
Op het tabblad Menging is ook te zien dat het schrijven van een differentiaal-vergelijking niets meer voorstelt; bovenaan staat een stukje uit mijn afstudeerscriptie, daar onder een Excel-formule.
Jammer dat ik nu nooit meer iets van doen heb met differentiaalvergelijkingen😉