
Het symbool hiernaast betekent ongeveer gelijk aan.
Als we met Excel aan het rekenen zijn, nemen we daar natuurlijk geen genoegen mee! Toch moeten we ons altijd bewust zijn van de beperkingen van dit hulpmiddel wat rekenen betreft.
In dit artikel zullen we aan de hand van enkele voorbeelden laten zien dat Excel zeker ‘rekenfouten’ maakt. Soms worden dit bugs in Excel genoemd, maar dat is niet juist: het is onder andere de consequentie van het binaire karakter van onze computers.
Uiteraard kijken we ook hoe we in ons dagelijks werk rekening kunnen houden met dit ‘vreemde’ gedrag van Excel (en ieder ander rekenprogramma).
‘Rekenfouten’
Nog steeds als ik een (simpel) rekenapparaat in handen krijg moet ik gauw even testen hoe nauwkeurig die werkt: 1 delen door 3, het resultaat vermenigvuldigen met 3 en van dat resultaat 1 aftrekken. Het resultaat zou dan 0 moeten zijn.
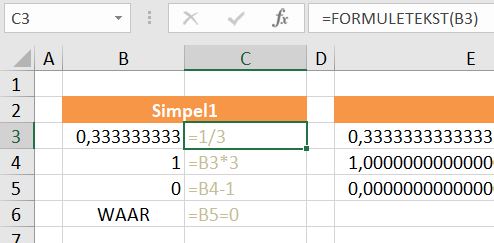
In het tabblad Simpel van het Voorbeeldbestand staat een dergelijke berekening. In cel B6 is te zien, dat Excel in ieder geval vindt dat het eindresultaat exact gelijk is aan nul.
NB1 in kolom C is de functie Formuletekst gebruikt; deze zet een eventuele formule in de cel, die je tussen de haakjes meegeeft (in het voorbeeld cel B3), om in een tekst. Deze functie bestaat vanaf Excel 2013.
NB2 als de betreffende cel geen formule bevat dan is het resultaat van deze functie #N/B (Niet Beschikbaar).
Dit kunt u op de volgende manier ondervangen: =ALS.FOUT(FORMULETEKST(B3);”Geen formule”)
Maar eigenlijk is het niet zo logisch, dat het resultaat nul is! We weten allemaal dat, als we de breuk 1/3 omzetten naar een decimaal getal, we nooit klaar zijn; het aantal drietjes achter de komma is oneindig.

In het tweede voorbeeld op het tabblad Simpel staat dezelfde berekening, maar nu zijn alle resultaten weergegeven met 20 decimalen.
Duidelijk is te zien, dat Excel bij het berekenen van 1/3 er na 15 decimalen mee ophoudt. In de dagelijkse praktijk kunnen we daar meestal ook wel mee leven.
Maar: als we dat resultaat weer met 3 vermenigvuldigen komt Excel toch op 1 uit en niet op 0,99999… Wie houdt nu wie voor de gek? Blijkbaar legt Excel intern het getal 1/3 anders vast dan wij zien. Dat is natuurlijk ook wel logisch: wij zijn gewend om te rekenen in het decimale stelsel, terwijl computers in het binaire stelsel maar tot 2 kunnen tellen, nog erger eigenlijk maar tot 1. Zij kunnen alleen maar werken met nullen en enen; voor gehele getallen kom je dan een heel eind (als je maar genoeg bits op een rijtje zet), maar bij decimale getallen komen computers al snel ‘in de problemen’.
Met dit in het achterhoofd is het eigenlijk verwonderlijk dat we niet iedere dag Excel op rekenfouten betrappen.
NB na wat googlen: “Excel werkt met een aangepaste 1985-versie van de IEEE 754 specificatie. De implementatie van Excel omvat conversies tussen binaire en decimale weergaven, wat leidt tot een nauwkeurigheid die gemiddeld beter is dan men zou verwachten van een eenvoudige 15-cijferige nauwkeurigheid.“
Nog een voorbeeld: we laten Excel 1/9 uitrekenen. Dit zou een getal met oneindig veel decimalen gelijk aan 1 moeten opleveren; ook hier laat Excel maar 15 eentjes zien.
Daar tellen we 1 bij op en van dat resultaat trekken we weer 1 af. Als we die uitkomst aftrekken van de eerste berekening komt er precies nul uit.

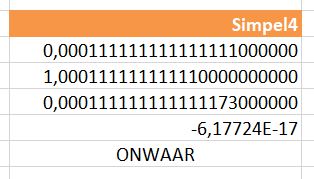
Maar doen we hetzelfde met 1/9000 dan komt er geen nul meer uit! Het resultaat is ‘veel’ groter dan waar we mee begonnen.
NB1 6,17E-17 is de zogenaamde wetenschappelijke notatie van een getal; dit betekent dat we 6,17 moeten vermenigvuldigen met 10 tot de macht -17 (10^-17) ofwel delen door 10^17 ofwel de 6 komt op de plaats van de 17e decimaal.
NB2 de notatie E-17 moet niet verward worden met de in de wiskunde gebruikte exponentiële functie e:![]()
Nog meer voorbeelden
Helaas is de reeks voorbeelden van ‘onverklaarbare rekenfouten’ in Excel schier onuitputtelijk. In het tabblad Vb van het Voorbeeldbestand vindt u er nog een paar:
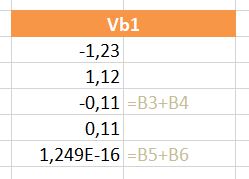

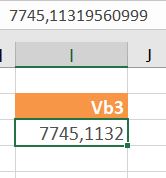
In Vb3 is het getal 7745,11319561 ingevoerd; Excel verandert dat op eigen houtje.
En wat te denken van het verschil tussen 7,11 en 7,1 of 7,11 en 7,01?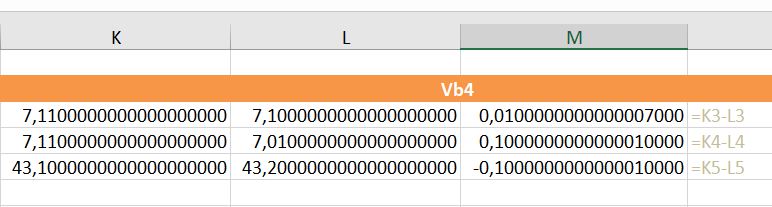
Hiernaast staat een simpele berekening: het tweede en derde getal worden afgetrokken van het eerste. Iedereen ziet direct dat daar 0 uit moet komen. Gelukkig: Excel is het daarmee eens.
Maar wat nu? In kolom Q doen we dezelfde berekening, maar tellen daar dan nog 0 (nul, zero, niente, nada) bij op. Het resultaat is schrikken.
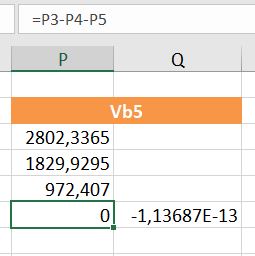
Het mag duidelijk zijn, dat we altijd alert moeten blijven bij resultaten van berekeningen in Excel. Ik kan me niet voorstellen, dat een bedrijf failliet gaat wanneer het laatste van 15 significante cijfers niet helemaal klopt. Maar er kunnen wel problemen ontstaan bij geautomatiseerde spreadsheets: verticaal zoeken levert verkeerde resultaten, controletellingen komen niet op nul uit, formules met Als leveren een foutieve uitkomst.
Afronden
Veel van de hierboven geschilderde problemen kunnen we oplossen door tussen- en/of eindresultaten af te ronden.
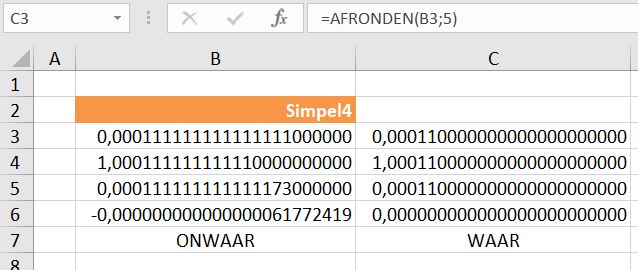
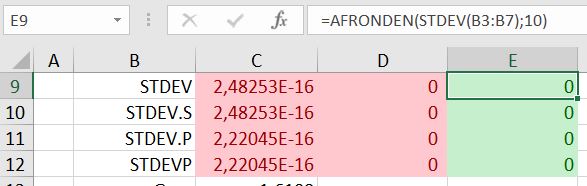
In het tabblad Afronden van het Voorbeeldbestand ronden we in kolom C iedere tussenstap van het vierde voorbeeld af op 5 decimalen.
NB 5 decimalen is ruim voldoende als het bijvoorbeeld een financieel overzicht betreft. De diverse eindresultaten dienen dan op 2 decimalen aan te sluiten.
Sneller, handiger en efficiënter is het om alleen de einduitkomst af te ronden: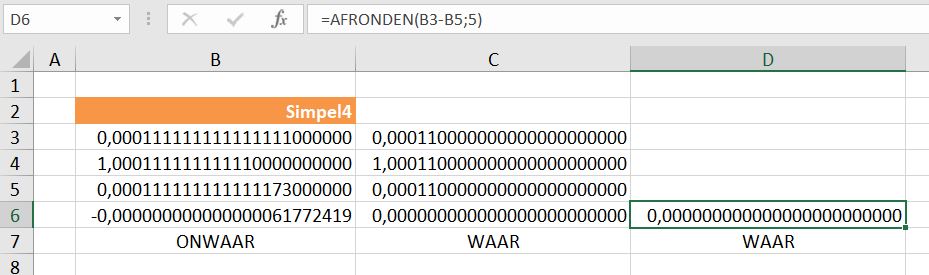
In het tabblad Afronden van het Voorbeeldbestand vindt u diverse overzichten waarmee u kunt zien wat de effecten van de verschillende afrondingsmethoden zijn. Ook ziet u daar de consequenties van negatieve waarden voor het aantal decimalen.
Wat als?
De aanleiding voor dit artikel was een vraag van iemand, die zich afvroeg waarom zijn metingen-systeem in Excel zich ‘ineens zo raar gedroeg’.
Per monster worden 5 metingen gedaan; om te bepalen hoe groot de spreiding van de metingen is wordt een standaarddeviatie berekend.
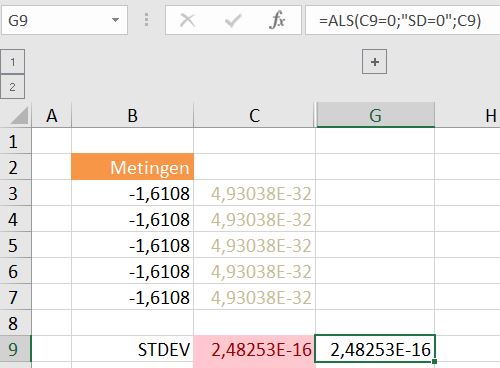
Omdat het regelmatig voorkomt dat de metingen allemaal dezelfde waarde opleveren moet dit zichtbaar gemaakt worden door weergave van de tekst SD=0. Blijkbaar is dit jaren goed gegaan maar ineens kwamen er vreemde resultaten.
In het tabblad SD van het Voorbeeldbestand zijn in kolom B vijf meetresultaten opgevoerd; allemaal de waarde -1,6108. In cel C9 is met de functie STDEV de standaarddeviatie hiervan bepaald.
Waar we nul zouden verwachten, blijkt Excel een kleine waarde te genereren, waardoor in cel G9 niet de verwachte tekst (SD=0) tevoorschijn komt.
NB1 de functie STDEV is een ‘oude’ functie, die uit comptabiliteitsoverwegingen nog in Excel gebruikt kan worden.
NB2 de functie STDEV berekent de deviatie voor een steekproef. De werking is dus gelijk aan de ‘nieuwe’ functie STDEV.S.
Voor het bepalen van de deviatie voor de hele populatie moet u de functie STDEV.P (nieuw) of STDEVP (oud) gebruiken.

Op het tabblad SD van het Voorbeeldbestand hebben de 4 deviatie-berekeningen een voorwaardelijke opmaak gekregen: als het resultaat nul is, dan wordt het vak groen gekleurd, anders rood.
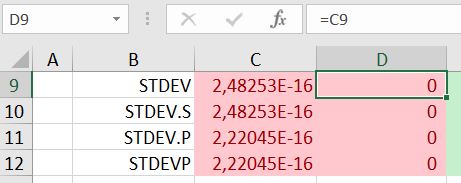
LET OP in kolom D staan dezelfde deviatiewaarden als in kolom C. De celeigenschappen hiervan zijn zodanig gewijzigd, dat er geen decimalen zichtbaar zijn. Nu lijkt het resultaat wel nul te zijn, maar de voorwaardelijke opmaak laat zien, dat dit niet zo is.
We hebben alleen de opmaak gewijzigd, niet de inhoud van de cel.
in cel G11: =ALS(AFRONDEN(C9;10)=0;”SD=0″;C9)
Wat te doen, als we toch de Als-functie willen gebruiken of voorwaardelijke opmaak aan cellen willen toevoegen?
Eén oplossing hebben we hiervoor al gezien: gebruik de functie Afronden.
Een andere methode is om binnen de Als-functie de mogelijke onnauwkeurigheid in te bouwen. In cel G10 staat de formule
=ALS(C9<0,00000000000001;”SD=0″;C9)
NB1 omdat een standaarddeviatie altijd positief is werkt bovenstaande formule prima. Als je niet zeker weet of de afwijking positief of negatief zal zijn dan is het beter om de volgende formule te gebruiken:
=ALS(ABS(C9)<0,00000000000001;”SD=0″;C9)
NB2 uiteraard hangt het van de situatie af, welke grens er in de vergelijking moet worden ingevuld. In dit geval zou de volgende formule ook voldoen:
=ALS(ABS(C9)<1e-10;”SD=0″;C9)
Allemaal gelijk of niet?
In het voorbeeld op het tabblad SD van het Voorbeeldbestand wordt de functie STDEV ook gebruikt om te beoordelen of alle metingen hetzelfde zijn.
Dat kan natuurlijk ook op een andere manier.
Hiernaast is in cel C18 de minimum-waarde van de metingen bepaald en in cel C19 het maximum.
In cel C20 wordt dan gekeken of deze twee gelijk zijn; zo ja dan zijn alle metingen gelijk.

Uiteraard is de tussenstap niet per se nodig. In cel D20 staat de formule:
=MIN(B3:B7)=MAX(B3:B7)
NB voor het bepalen van het minimum en maximum hoeft Excel geen berekening uit te voeren. We hoeven dus niet ‘bang te zijn’ dat Excel een extra onnauwkeurigheid toevoegt.

