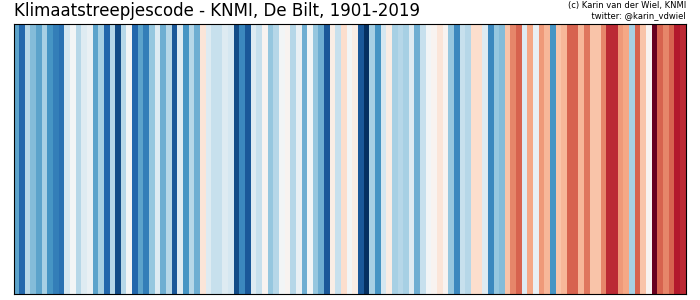
Het KNMI publiceerde vorige week een klimaat-streepjescode. Zonder veel extra informatie is direct te zien wat de hoofdconclusie is!
Behalve dat de achterliggende oorzaak niet blij-makend is, is dit wel een mooie aanleiding om te kijken of we in Excel een dergelijk overzicht kunnen maken.
Brongegevens
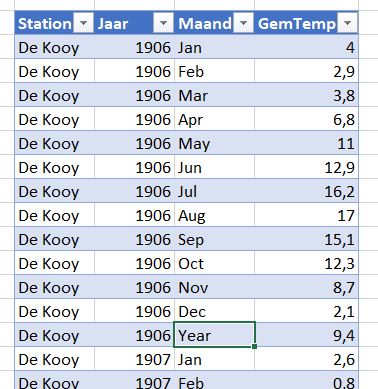
Het KNMI stelt van een 10-tal weerstations de historische gemiddelde temperaturen ter beschikking; gemiddeld per jaar en per maand.
In het tabblad Data van het Voorbeeldbestand staat een link naar één van de bestanden.
Met behulp van Power Query (zie dit artikel) zijn deze bestanden binnengehaald en in één totaal-tabel, tblBronData, geplaatst (zie het tabblad Brondata van het Voorbeeldbestand).
Jaar-overzicht
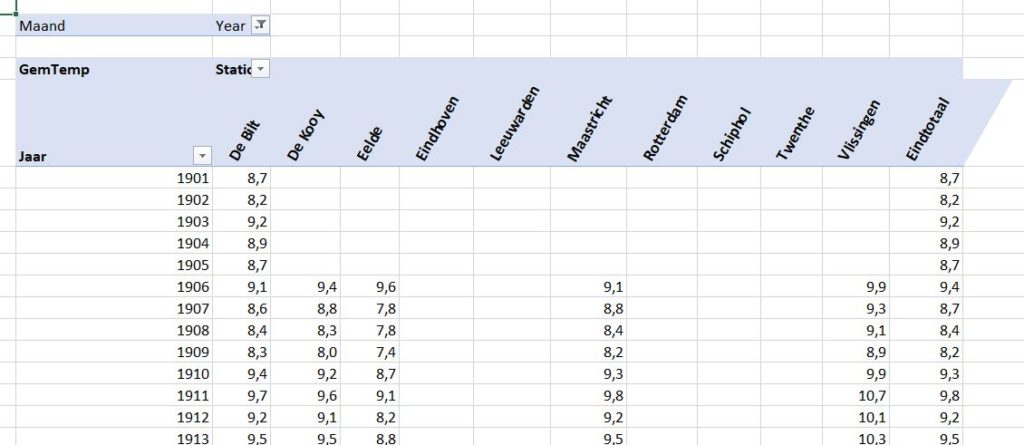
Het tabblad OvzJr van het Voorbeeldbestand bevat een draaitabel gemaakt op basis van deze brongegevens. In het filterblok hebben we alleen voor jaarcijfers gekozen.
Nu is snel te zien dat de meeste weerstations pas cijfers vanaf 2006 hebben. Ook zien we dat Nederland nog een behoorlijke variatie in de gemiddelde temperatuur kent (gemiddeld over alle jaren een verschil van 1,5 graad tussen Eelde en Vlissingen).
Enkele stations hebben geen cijfers voor de jaren 1944 en 1945.
NB1 de Waardeveldinstellingen van de gemiddelde temperatuur is gewijzigd van de standaardinstelling Som naar Gemiddeld, zodat in de eindkolom een gemiddelde over alle stations ontstaat.
NB2 de tekst Gemiddelde van GemTemp linksboven in de tabel is gewijzigd; wel staat er een spatie achter GemTemp, anders geeft Excel een foutmelding.
Maand-overzicht
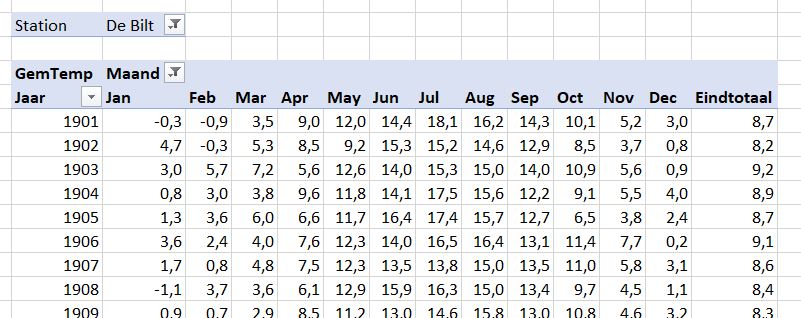
In het tabblad OvzMnd van het Voorbeeldbestand is een andere draaitabel op basis van de brongegevens gemaakt. Per weerstation zijn daar de maandgemiddelden per jaar terug te vinden.
NB bij Maand is het item Year uitgevinkt.
Maandgrafiek
Meestal geeft een grafiek een beter inzicht in het verloop in de tijd dan een tabel met getallen.
In het tabblad GrafMnd van het Voorbeeldbestand ziet u het resultaat:
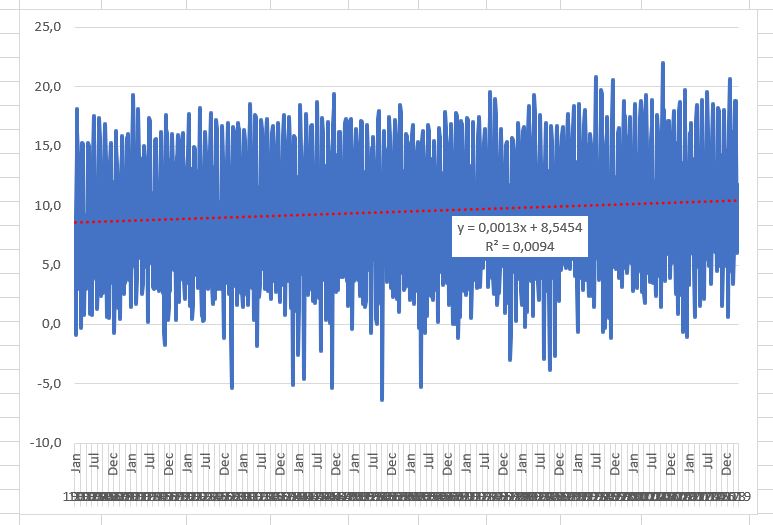
Door de grote hoeveelheid gegevens valt hier weinig te concluderen. Wel hebben we een (lineaire) trendlijn toegevoegd (rechts-klikken op de grafiek) en dan zien we dat er een stijgende lijn is. Voor iedere stap op de x-as (dus iedere maand) gaat de temperatuur gemiddeld 0,0013 graad omhoog; dat is per jaar dus ruim 0,015 graden en per 100 jaar 1,5 graad, ruwweg de spreiding van het gemiddelde over Nederland.
NB de ![]() is een maat voor de betrouwbaarheid van de trendlijn; hoe dichter bij 1 hoe beter. Zie het artikel Trend-analyse.
is een maat voor de betrouwbaarheid van de trendlijn; hoe dichter bij 1 hoe beter. Zie het artikel Trend-analyse.
Jaargrafiek
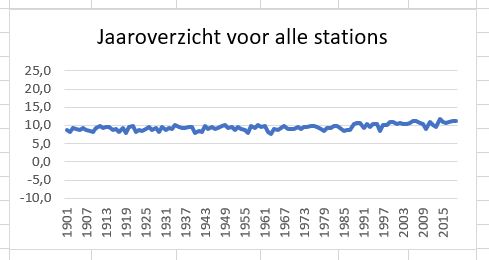
Dan maar de maandgegevens weglaten en ons focussen op het jaargemiddelde.
Dat zegt nog steeds niet veel (zie het tabblad GrafJr van het Voorbeeldbestand).
Daarom de y-as wat aanpassen zodat de variaties per jaar beter zichtbaar worden:
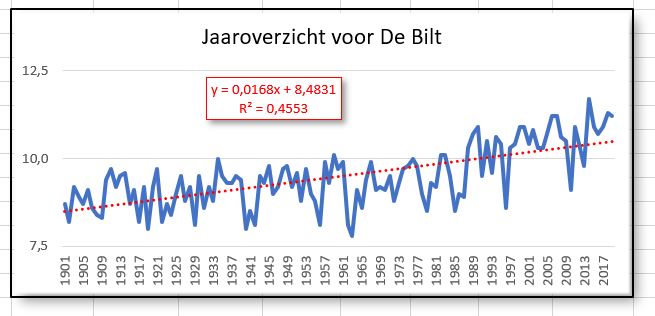
Duidelijk is te zien dat het jaargemiddelde een stijgende lijn vertoont, ondanks de diverse uitschieters naar beneden.
De stijging van de trendlijn is bijna 0,017 graad per jaar; de betrouwbaarheid is natuurlijk vele malen groter omdat we alleen naar het jaar-gemiddelde kijken.
NB dit artikel gaat niet over trendanalyse; misschien is een lineaire trend hier niet de meest relevante.
Klimaat-streepjescode
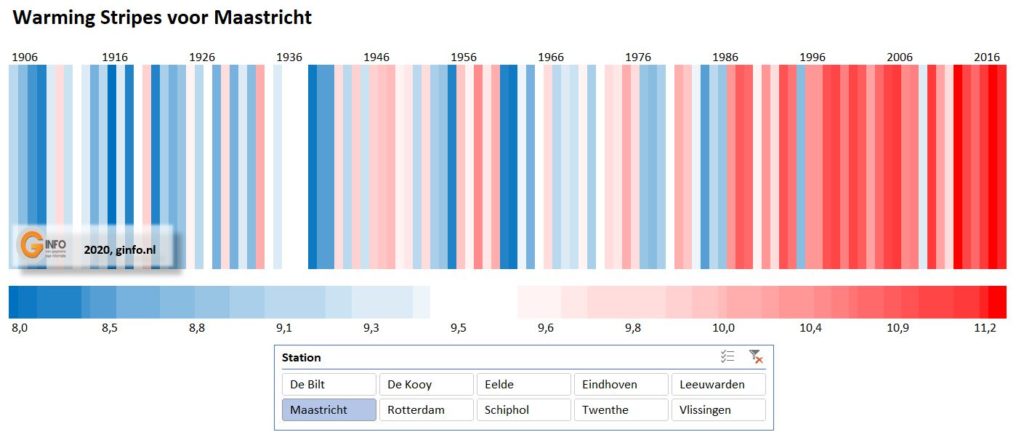
Deze manier om klimaatdata weer te geven is bedacht door klimaatwetenschapper Ed Hawkins (onder de naam ‘warming stripes’); dit om de langjarige trend van temperaturen onder de aandacht te brengen.
Maar hoe maken we dit in Excel? Het lijkt op een grafiek maar is het niet; we gaan Voorwaardelijke opmaak gebruiken (zie het tabblad WarmStr in het Voorbeeldbestand):
- we maken een draaitabel net als in het tabblad GrafJr, maar we zorgen er voor dat de jaren naast elkaar komen (dus plaatsen Jaar in de Kolommen).
NB door een kopie te maken van de draaitabel lopen de filteringen/selecties, die we later toepassen, synchroon. De draaitabellen laten allemaal dezelfde gegevens zien maar op een andere manier. - in rij 4 staat om de 10 cellen een verwijzing naar rij 9 (de jaren)
- zorg dat in het Filterblok alle stations zijn gekozen en selecteer dan alle gevulde cellen in rij 10.
- kies in de menutab Start in het blok Stijlen de optie Voorwaardelijke opmaak
- kies bij Kleurenschalen de zesde optie (rood-wit-blauw)
- maak de kolommen smaller en rij 10 hoger
- zorg dat rijen en kolommen, die het beeld ‘vertroebelen’, niet zichtbaar zijn. Selecteer de betreffende rijen (of kolommen) en kies in de menutab Gegevens in het blok Overzicht de optie Groeperen.
NB1 gebruik Groeperen en NIET Verbergen. Een groot nadeel van de 2e methode is namelijk dat anderen (en jijzelf!) niet in de gaten hebben dat er iets niet zichtbaar is.
NB2 wil je de kleuren aanpassen? Ga naar Voorwaardelijke opmaak/Regels beheren.

Maak een kopie van de draaitabel, plaats die er onder en sorteer die op oplopende waarde van de gemiddelde temperatuur en u hebt een mooie temperatuurlegenda. Deze verandert automatisch mee bij verandering van weerstation-keuze.
Analyse
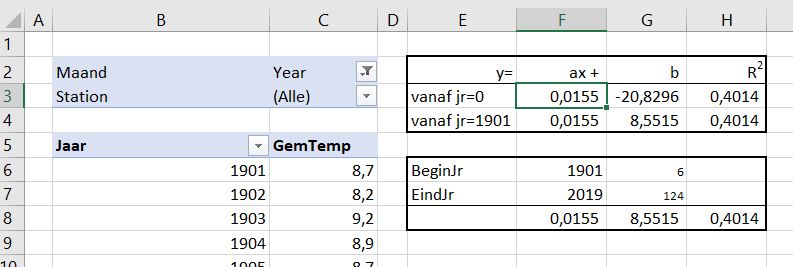
Maar we kunnen de trend binnen de basisgegevens nog verder (en preciezer) analyseren (zie het tabblad Analyse van het Voorbeeldbestand).
De richting van de trendlijn kunnen we ook bepalen zonder de trendlijn te tekenen:
=RICHTING(C6:C124;B6:B124)
De waarde voor b in de formule voor de rechte lijn bepalen we op een vergelijkbare manier met de functie Snijpunt.
NB Snijpunt bepaalt de waarde voor b in het jaar 0 (nul). In cel G4 staat een gecorrigeerde formule, zodat b de waarde geeft voor het eerste jaar uit de reeks (in het voorbeeld 1901): =SNIJPUNT(C6:C124;(B6:B124)-B6+1)
De ![]() wordt bepaald met de functie R.KWADRAAT.
wordt bepaald met de functie R.KWADRAAT.
Om de richting van de trend (en de bijbehorende ![]() ) op bepaalde tijdsintervallen te kunnen bepalen heb ik nog een apart blokje berekeningen toegevoegd:
) op bepaalde tijdsintervallen te kunnen bepalen heb ik nog een apart blokje berekeningen toegevoegd:
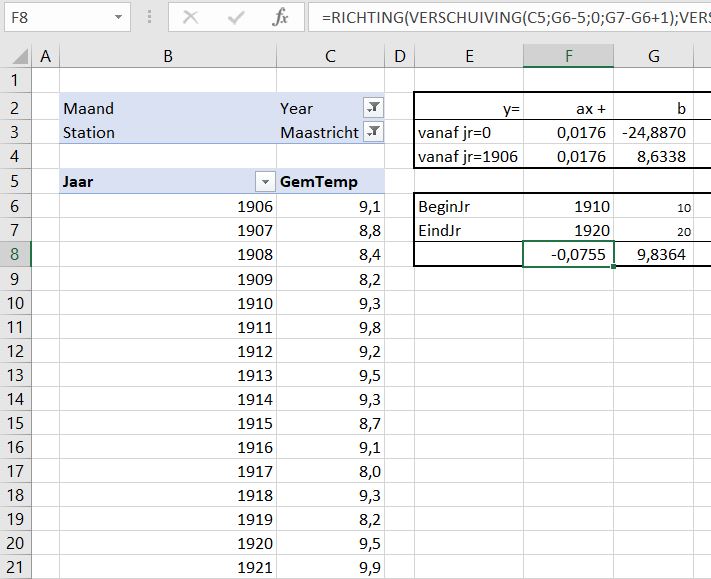
Via een begin- en eindjaar wordt bepaald welke rijen uit de kolommen B en C we in de berekening mee willen nemen (in het voorbeeld hier de rijen 10 t/m 20). Bij het berekenen van de richting nemen we het betreffende blok mee door middel van de functie Verschuiving:
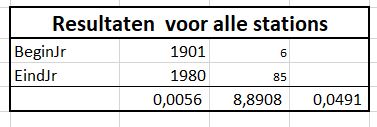
Bekijken we de gemiddelde resultaten voor heel Nederland tot en met 1980 , dan zien we dat de gemiddelde jaarlijkse temperatuurstijging op 0,0056 uitkomt met een lage betrouwbaarheid.
Terwijl de gemiddelde stijging in de laatste 40 jaar bijna een factor 10 groter is. Daarbij is de betrouwbaarheid van die trend ook een factor 10 hoger.