 Excel is inzetbaar op veel gebieden; ook binnen het (wiskunde-)onderwijs is het goed bruikbaar.
Excel is inzetbaar op veel gebieden; ook binnen het (wiskunde-)onderwijs is het goed bruikbaar.
Ik moest daar deze week aan denken, toen ik bedacht hoe ik 20 jaar geleden met iemand tijdens bijlessen heb zitten worstelen om hem het gevoel bij te brengen hoe 1e- en 2e-graads-functies er in grafiekvorm uitzien.
Eerstegraadsfunctie
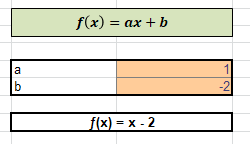 Zoals we allemaal (?) weten is de algemene vorm van een eerstegraadsfunctie zoals hiernaast weergegeven.
Zoals we allemaal (?) weten is de algemene vorm van een eerstegraadsfunctie zoals hiernaast weergegeven.
Door voor a en b waarden in te vullen krijg je een specifieke functie.
In het Voorbeeldbestand in het tabblad 1e graads is de algemene functie ingevoerd door in de menutab Invoegen in het blok Symbolen de optie Vergelijking te kiezen.
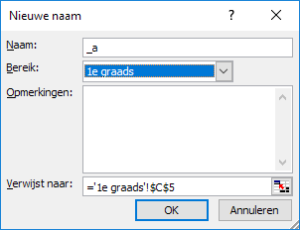 De cellen C5 en C6 (naast de teksten a en b) hebben een naam gekregen:
De cellen C5 en C6 (naast de teksten a en b) hebben een naam gekregen:
- kies de menutab Formules
- dan in het blok Gedefinieerde namen de optie Naam definiëren
- voer een Naam in, in dit geval _a
- kies een Bereik. Standaard is de naam geldig voor de hele Werkmap, maar in dit geval moet het bereik beperkt worden tot het werkblad 1e graads
- pas zo nodig de verwijzing nog aan en klik op OK
NB Excel accepteert niet alle letters als Naam; ik heb er in dit geval voor gekozen om alle namen door een _ (underscore) te laten voorafgaan.
In cel B8 wordt de functie tekstueel opgebouwd:
=”ƒ(x) = ” & ALS(_a=0;””;ALS(_a=1;”x”;ALS(_a=-1;”-x”;_a&”x”))) & ALS(_b=0;””;ALS(_b<0;” – “;” + “) & ABS(_b))
De diverse tekstblokken worden m.b.v. het &-teken aan elkaar gekoppeld.
In het eerste blok is de ƒ ingevoerd via Invoegen/Symbool. Kies daar allereerst rechtsonder de optie ASCII (decimaal) en blader dan door de mogelijkheden.
Wiskundige tekens kunnen ook op de volgende site gevonden worden: Lijst_van_wiskundige_symbolen; gebruik daar kopiëren en plak dan in Excel.
Met de diverse ALS-functies wordt de opmaak geregeld, zodat er bijvoorbeeld geen 0x of 1x in het resultaat komt te staan.
De ABS-functie levert de absolute waarde van een getal; het resultaat is dan altijd groter of gelijk aan 0.
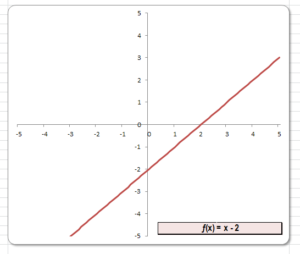 Om de grafiek te kunnen tekenen hebben we een tabel nodig met de bij de functie horende x,y-waarden. In het tabblad 1e graads van het Voorbeeldbestand worden 100 combinaties berekend in de cellen vanaf B32. In cel C32 komt dan de formule =_a*B32+_b
Om de grafiek te kunnen tekenen hebben we een tabel nodig met de bij de functie horende x,y-waarden. In het tabblad 1e graads van het Voorbeeldbestand worden 100 combinaties berekend in de cellen vanaf B32. In cel C32 komt dan de formule =_a*B32+_b
NB Om het effect van veranderingen in a of b goed te kunnen zien zijn de assen ‘vastgezet’: ze lopen allebei van -5 tot +5.
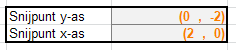 Bij eerstegraadsfuncties zijn de snijpunten met de assen altijd belangrijk. Die worden in de cellen C10 en C11 berekend met de formules =”(0 , “&_b&”)”, respectievelijk =ALS(_a=0;”geen”;”(“&-_b/_a&” , 0)”)
Bij eerstegraadsfuncties zijn de snijpunten met de assen altijd belangrijk. Die worden in de cellen C10 en C11 berekend met de formules =”(0 , “&_b&”)”, respectievelijk =ALS(_a=0;”geen”;”(“&-_b/_a&” , 0)”)
Omdat het resultaat van de laatste formule vaak geen geheel getal oplevert, is het inzichtelijker om het resultaat zo nodig als een breuk weer te geven (zie cel C15):
=ALS(_a=0;”geen”;”(“&TEKST(-_b/_a;”# ??/??”)&”, 0)”)
M.b.v. de functie TEKST wordt een opmaak meegegeven aan het resultaat -b/a: eventueel een geheel getal (#) en als het nodig is een breuk (met maximaal 2 cijfers in de teller en noemer).
Om alle overbodige spaties te verwijderen, kan de functie SUBSTITUEREN worden gebruikt (zie bijvoorbeeld cel C19 in het tabblad 1e graads).
 In de grafiek is ook de functie weergegeven. Dit is als volgt gedaan:
In de grafiek is ook de functie weergegeven. Dit is als volgt gedaan:
- selecteer de cel met de functie en kies kopiëren (Ctrl-C)
- klik ergens anders op het werkblad met de rechter muistoets
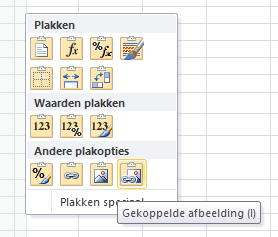
- kies Plakken speciaal …
- en in het vervolgscherm de laatste optie van Andere plakopties (Gekoppelde afbeelding)
De inhoud van de oorspronkelijke cel wordt dan dynamisch in een grafisch object weergegeven. Dit object kan via slepen overal in de sheet geplaatst worden, dus ook in de grafiek.
Tweedegraadsfunctie
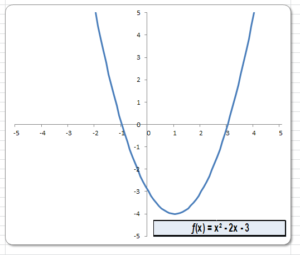
 De opbouw van het tabblad 2e graads van het Voorbeeldbestand is vergelijkbaar met bovenstaande.
De opbouw van het tabblad 2e graads van het Voorbeeldbestand is vergelijkbaar met bovenstaande.
Het bepalen van de eventuele snijpunten met de x-as is echter wat ingewikkelder. Weet u nog?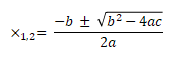
 Maar dit levert alleen maar een resultaat op als het getal onder de wortel (de discriminant) niet kleiner is dan nul; dus dat wordt eerste even gecontroleerd.
Maar dit levert alleen maar een resultaat op als het getal onder de wortel (de discriminant) niet kleiner is dan nul; dus dat wordt eerste even gecontroleerd.
In C14 staat daarom de volgende formule:
=ALS(Oplos?=”geen”;”geen”;”(“&(-_b-WORTEL(Discr))/(2*_a)&” , 0)”)
Derdegraadsfunctie
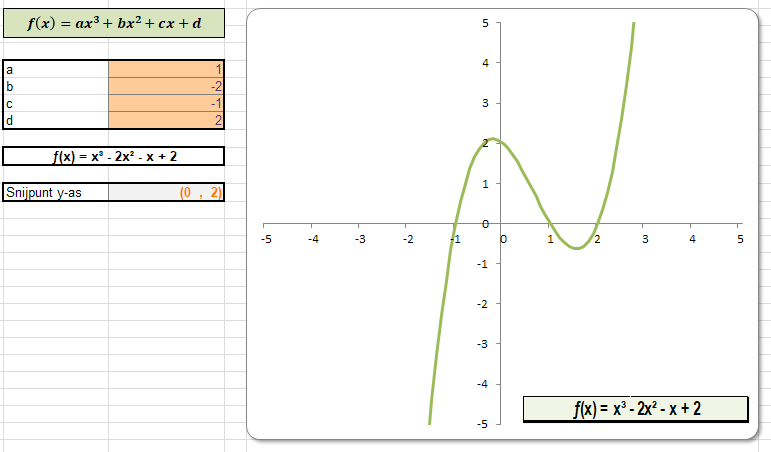 In het tabblad 3e graads van het Voorbeeldbestand wordt de grafiek van een derdegraadsfunctie weergegeven. Het bepalen van de snijpunten met de x-as wordt nu wat lastiger; dat valt buiten de scope van dit artikel.
In het tabblad 3e graads van het Voorbeeldbestand wordt de grafiek van een derdegraadsfunctie weergegeven. Het bepalen van de snijpunten met de x-as wordt nu wat lastiger; dat valt buiten de scope van dit artikel.

